Человеческий фактор на ЕГЭ по математике профильного уровня

После длительного перерыва, вызванного техническими проблемами, продолжаем работу сайта.

После длительного перерыва, вызванного техническими проблемами, продолжаем работу сайта.
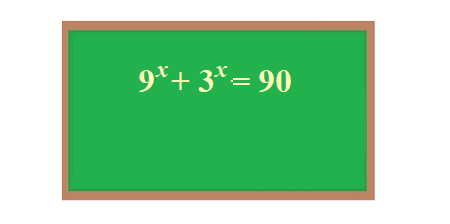
На фото ниже приведён заключительный кадр видео. Хорошо видно, как автор решения выполняет замену неизвестного, решает квадратное уравнение с новым неизвестным, отбирает один корень и выполняет обратную замену неизвестного. Показать, как найти корень уравнения и что он единственный, можно именно так.

А.В. Шевкин, avshevkin@mail.ru
Доктор физ.-мат. наук, член-корр. РАН А. В. Савватеев поделился с коллегами по объединению «Родная школа» ответом, полученным им из Рособрнадзора 24.04.2023 по поводу ЕГЭ. Письмо вызывает возражения и требует комментариев, поэтому копирую фрагменты письма (курсивом) и комментирую.

Данная заметка была опубликована на канале Наблюдатель (на Дзене), но там была заблокирована. Возможно, толерантный Дзен посчитал, что своей заметкой я вызываю вражду. Я с этим категорически не согласен и публикую заметку на своём ресурсе, чтобы сослаться на эту публикацию на Дзене.

Вчера в 18:00 состоялся Круглый стол Национального центра помощи детям, на котором я не планировал выступление, но пока говорили два первых докладчика, захотелось включиться в разговор, я набросал несколько тезисов, которые потом дополнил интересными цитатами – уже после спонтанного выступления.

Учащиеся иногда сталкиваются с непривычными иррациональными уравнениями, содержащими корни степени выше второй. В этом случае полезно помнить, то эти уравнения могут оказаться «на лицо ужасными, но добрыми внутри» — как люди-дикари с «Острова Невезения». Рассмотрим пример.

Рассмотрим решение задачи с параметром из сборника для подготовки к ЕГЭ-2023 профильного уровня [1]. Первоначально статья печаталась на сайте, но внимательные читатели указали на ошибку в решении.

А. В. Шевкин, avshevkin@mail.ru
Повторяем листок с заданиями олимпиады, приношу извинения за качество фото, предоставленного нашим источником. Если найдёте более качественный текст, то прошу прислать ссылку на него на адрес моей электронной почты.
Под заметкой по математике, которые на канале мало кто читает, появилась задача, заданная сыну читателя. С неё начинаем рубрику «Задачи по заявкам читателей».

На днях прислали мне для ознакомления текст олимпиады по математике, которая состоялась 25 марта в лицее № 131 Вахитовского района г. Казани.