Репетиционный экзамен. ГУУ-2000

Готовящиеся сейчас сдавать профильную математику на ЕГЭ гоняют варианты однотипных заданий, а мы предлагаем взглянуть на стародавние варианты.

Готовящиеся сейчас сдавать профильную математику на ЕГЭ гоняют варианты однотипных заданий, а мы предлагаем взглянуть на стародавние варианты.
Вчера состоялся мой разговор с учителем информатики школы № 564 Адмиралтейского района Санкт-Петербурга, председателем Санкт-Петербургского городского родительского комитета Михаилом Юрьевичем Богдановым.

Очень интересный опрос мнений придумала вице-губернатор Санкт-Петербурга, Ирина Петровна Потехина. Про отношение родителей к ЕГЭ, как к инструменту поступления в ВУЗы.

1 июня 2021 в возрасте 81 года после тяжелой болезни ушел из жизни доктор физико-математических наук, профессор кафедры математики физического факультета МГУ, научный руководитель СУНЦ МГУ Валентин Федорович Бутузов.
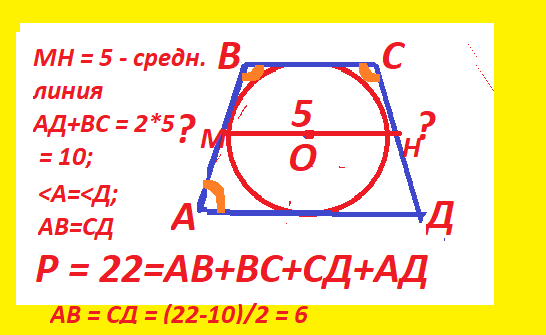
Я уже писал заметку Задачи про несуществующие треугольники.

7 мая 2021 г. завершено кулуарное обсуждение Федерального государственного образовательного стандарта основного общего образования — ФГОС 4.0 [1].

Несколько дней назад в СМИ прошла информация о том, что 22 мая 2021 года Общественное движение «Родители Москвы» проводит Всероссийскую конференцию «Пути преодоления кризиса в образовании. Консолидация родительских и научных сообществ России».
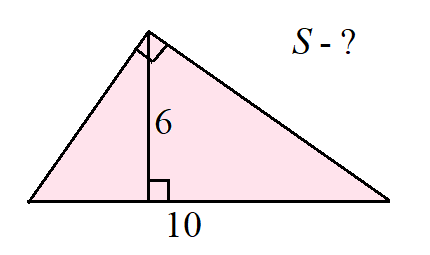
Известна задача из американского теста.
1. Найдите площадь прямоугольного треугольника, гипотенуза которого равна 10, а высота, проведённая к гипотенузе, равна 6.
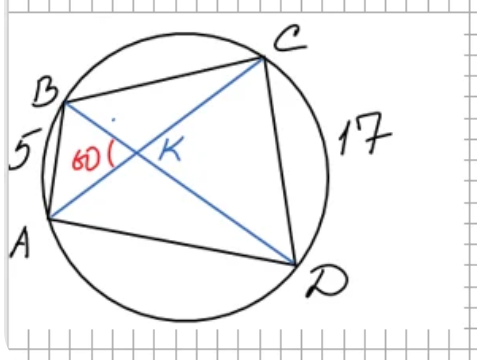
Рассмотрим хорошую задачу из заметки Теорема синусов и косинусов в одной задаче. Задача № 25 ОГЭ. Решим её и без теоремы синусов, и без теоремы косинусов.

МОСКВА, 19 мая 2021, 08:40 — REGNUM. Отрицательно к Единому государственному экзамену (ЕГЭ) относятся почти 70 % жителей России, свидетельствуют результаты опроса сервиса по поиску высокооплачиваемой работы SuperJob.