Выпускной экзамен 2006 года (11 ФМК)

В разговорах про ЕГЭ по математике очень часто можно услышать, что без ЕГЭ никак нельзя, что же это будет за проверка…

В разговорах про ЕГЭ по математике очень часто можно услышать, что без ЕГЭ никак нельзя, что же это будет за проверка…

Рассмотрим задачи, связанные с одной задачей (№ 2) из конкурса «Кенгуру – 2020». Она предлагалась учащимся 9-10 классов в тестовой форме (ссылка ниже), но нас интересует и обоснование решения.

В данной заметке речь пойдёт о выборе способа решения геометрической задачи. До разбора конкретного примера надо сказать несколько общих слов.

Мне прислали хорошую задачку олимпиадного уровня для пятиклассников, которая включена то ли в реальный текст, то ли в текст для подготовки к ВПР.
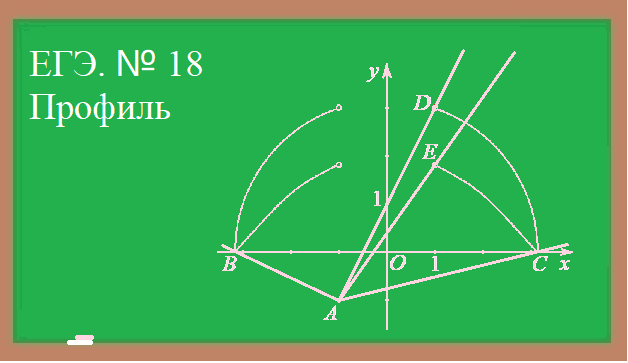
Рассмотрим задание 18 из варианта 14 сборника для подготовки к ЕГЭ [1].
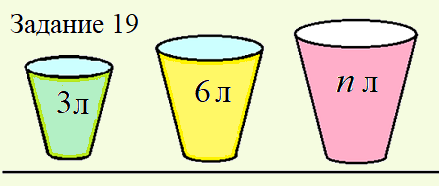
Про задачи на переливания я уже писал три раза, так как в сборниках для подготовки к ЕГЭ в задаче 19 (в) была неточность и ответ не соответствовал условиям задачи.
В книге [1] есть задачи про функцию, которые не часто задают в школе. Давайте разберём их решения. Но сначала выполним подготовительные задания.
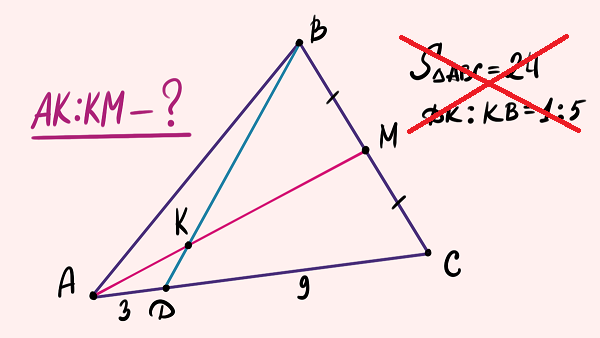
Начнём с задачи на нахождение отношения длин отрезков в
треугольнике.

Вчера у меня был волнительный день: перешёл в категорию 70+.