Вокруг одной задачи конкурса Кенгуру–2020 для 9-10 классов

Рассмотрим задачи, связанные с одной задачей (№ 2) из конкурса «Кенгуру – 2020». Она предлагалась учащимся 9-10 классов в тестовой форме (ссылка ниже), но нас интересует и обоснование решения.
Начнём с подготовительной задачи. Задачи 2 и 3 решите самостоятельно. Латинская буква a заменяет в тексте греческую букву альфа.
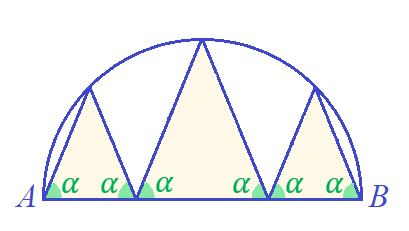
1. Шестизвенная ломаная вписана в полуокружность с диаметром АB. Каждый из углов между звеньями ломаной и диаметром AB равен a. Чему равен угол a?
Прежде всего отметим, что мы имеем три равнобедренных треугольника, причём треугольники AEN и BCK равны, так как точки C и E симметричны относительно диаметра окружности, перпендикулярного прямой AB.
Построим вторую полуокружность, пусть лучи EN и CK пересекаются в точке M. Эта точка лежит на окружности, что следует из равенства треугольников NMK и NDK. Углы AEM и BCM равны, они измеряются половинами угловых величин (90°) равных дуг AM и MB. Следовательно, углы при вершине равнобедренных треугольников равны 45°. Тогда углы a равны 67,5°.
2. Восьмизвенная ломаная вписана в полуокружность с диаметром АB. Каждый из углов между звеньями ломаной и диаметром AB равен a. Чему равен угол a?
3. Десятизвенная ломаная вписана в полуокружность с диаметром АB. Каждый из углов между звеньями ломаной и диаметром AB равен a. Чему равен угол a?
Искать здесь: https://050.mathkang.ru/page/files-k

Дополнение от 3.04.2021. Давайте посмотрим на рисунок к задаче 3.
Мы увидим три вписанных угла величиной бетта, опирающихся на дугу AKB, содержащую 180 градусов. Угол AGL равен 180 : 3 : 2 = 30 градусов. Тогда искомый угол GAB равен (180 — 30) : 2 = 75 градусов.
Для задачи в тестовой форме этого решения достаточно, для полного решения его надо немного дополнить.
