С праздником Октября!
С праздником поздравляю всех, кто помнит этот праздник. Красный день календаря советской эпохи.
Профессор А.В. Савватеев выступил перед учителями в Новосибирске
Это выступление было посвящено контр-реформе образования. Слово «реформа» за 30-40 лет изгажено так, что что-то менять в образовании под этим словом уже невозможно.
Доклад Анны Швабауэр о цифровых экспериментах в образовании
Доклад рекомендую читать в первоисточнике, так как там много слайдов презентации, есть ссылка на видео, он интересен целиком, а не в виде фрагментов. Ценность доклада заключается в том, что в нём показана методика проведения «фальшивых» как бы экспериментов, которые у нас проводят, начиная с эксперимента по ЕГЭ.
«Пророк» в своём отечестве
Давненько я наблюдаю за карьерным взлётом фантазёра из АСИ, а теперь спецпредставителя президента РФ по развитию и цифровизации, орденоносца Д. Н. Пескова.
Зачем журналисту математика?
В Комсомольской правде опубликована статья, в которой написано:
«Математика стала одним из самых любимых предметов у студентов факультета журналистики МГУ. Хотя еще 10-20 лет назад некоторые студенты шли учиться на журналистов именно потому, что в программе обучения математики не было вообще.
Запретить русский язык на Украине?
На своём сайте Шевкин.ру я стараюсь не размещать материалов, далёких от образования, от школьной математики. Эта статья — исключение. Её закрыла цензура ИИ Дзена — то ли за «язык вражды» (они хотят, чтобы материалы не вызывали резкой реакции читателей), то ли от большой доли цитированных материалов, этого они мне ещё не объяснили. Размещаю статью здесь, чтобы сделать на неё ссылку на Дзене.
Про американские глупости в образовании и наш образовательный стандарт
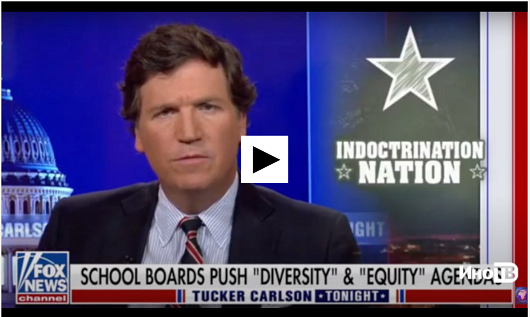
Начнём с сообщения о том, что в США поставили выше арифметики, то есть выше нормального образования. Ответ простой: воспитание послушных баранов, которые ничего не знают, ничего не умеют, в силу чего нуждаются в постоянном руководстве — пожизненно. Там у них уже отлажена технология для массового обучения. О наших проблемах поговорим потом. А пока читаем новость.
Образование после пандемии у них и у нас
Удивительные результаты показало отечественное образование после пандемии. На итоговых испытаниях в прошлом году было падение результатов на ОГЭ (по математике, 9 класс), а на ЕГЭ — нет, даже улучшение результатов по некоторым предметам. Можно подумать, что обучение на удалёнке не ухудшило качество образования, хотя такого не может быть, потому что не может быть никогда.
Письмо из Киева всем русским
Уважаемые читатели нашего сайта. Я стараюсь не размещать излишне политизированных текстов на этом сайте, который скоро отметит 20 лет своей работы. Но сегодня особенный случай. Размещаю здесь письмо, которое было закрыто на Яндекс.Дзене по соображениям «толерантности».
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171