Можно и без теоремы синусов, и без теоремы косинусов
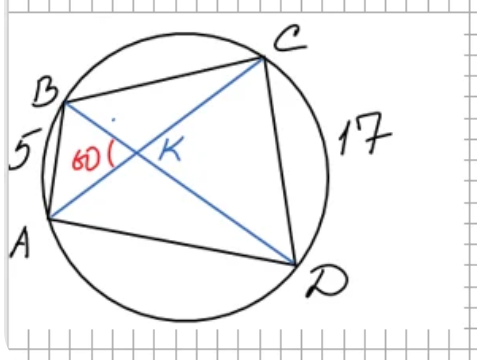
Рассмотрим хорошую задачу из заметки Теорема синусов и косинусов в одной задаче. Задача № 25 ОГЭ. Решим её и без теоремы синусов, и без теоремы косинусов.
Сначала поправим заголовок у коллеги. Речь идёт о двух теоремах, а не об одной.

Замечания от 22.05.2021
1. Переход от квадрата синуса к синусу в решении не обоснован ввиду очевидности, но на экзамене лучше написать, что угол x меньше 30 градусов, его синус положительный.
2. Автор заметки совершенно справедливо указал, что синуса разности ещё нет в общеобразовательном 9 классе. Поэтому обойтись без двух теорем — это почти спортивное развлечение. Ученику, не изучавшему синуса разности можно посоветовать такое рассуждение.
Угол BKA не изменится, если мы хорду AB сдвинем по окружности. Дуги AB и CD в сумме будут содержать 120 градусов. Рассмотрим крайний случай, когда точки B и C совпадут. В этом случай большая дуга AC будет содержать 240 градусов, а вписанный угол ABD — 120 градусов. По теореме косинусов вычислим длину отрезка AC, а потом по следствию из теоремы синусов найдём радиус окружности.
