Олимпиада Гаусса. 6 класс. Обсуждаем решения задач

А. В. Шевкин, avshevkin@mail.ru
Повторяем листок с заданиями олимпиады, приношу извинения за качество фото, предоставленного нашим источником. Если найдёте более качественный текст, то прошу прислать ссылку на него на адрес моей электронной почты.
Решения задач
Задача 1.
Задача 2. Число, составленное из 30 троек, слишком большое для утроения цифр с разряда единиц. Начнём утроение со старшего разряда и понаблюдаем. Записываем утроения одной цифры старшего разряда, остальные тройки «отдыхают»: 3, 9, 27, 41, 43.
В старший разряд вернулась тройка, а перед ней появилась цифра 4. Продолжим: 3, 9, 27, 41, 43, 49, 67, 81, 83.
Второе возвращение цифры 3 в старший разряд увеличивает на 4 число, записанной цифрой перед старшим разрядом. Через 8 таких возвращений перед старшей цифрой получится желанное число 32. Остальные 29 троек даны для сбивания с толку решателя задачи.
Ответ. Да.
Задача 3. В любой партии у любых игроков разной силы обязательно будет один победитель и один проигравший, он выбывает из дальнейшей игры.
Если всех игроков разбить на пары и провести сначала 8 игр (первый тур), потом опять разбить на пары провести 4 игры (второй тур), оставшихся четырёх игроков разбить на пары и провести ещё две игры (третий тур), то останутся два игрока, среди которых есть сильнейший, но ещё не известно, кто именно. Возможно, что это два сильнейших игрока.
Но возможно, что второй по силе игрок встретился с самым сильным игроком и выбыл в первом, или во втором, или третьем туре.
Проведём четвёртый тур среди двух победителей третьего тура. Он выявит сильнейшего. А второй по силе игрок мог выбыть в игре с сильнейшим в любом из четырёх туров.
Выбираем всех четырёх игроков, проигравших сильнейшему и среди них за три партии выбираем сильнейшего. Он окажется вторым по силе игроком. Всего потребуется 8 + 4 + 2 + 1 + 2 + 1 = 18 партий.
Ответ. Да.
выявления не хватит оставшихся пяти партий (требуется 6 партий).
Ответ. Нет.
Задача 4. Пусть трёхзначное число записано цифрами a, b, c и равно
100a + 10b + c. Составим уравнение по условиям задачи:
3(100a + 10b + c) + (a + b + c) = 4(100c + 10b + a),
300a + 30b + 3c + a + b + c = 400c + 40b + 4a,
297a = 396c + 9b,
33a = 44c + 9b,
33a – 44c = 9b,
11(3a – 4c) = 9b.
Число 9 не делится на 11. Число b однозначное, оно делится на 11, лишь при условии b = 0, тогда должно выполняться равенство 3a – 4c = 0.
Это возможно лишь при a = 4, c = 3 или при a = 8, c = 6.
Ответ. 403, 806.
Задача 5. Проиграет тот, кто последним ходом получит 1 треугольник, значит, чтобы не проиграть следующим ходом, надо отдавать сопернику фигуру, от которой нельзя отрезать треугольник. Все углы у неё должны быть тупыми. Выигрывает тот, кто отдаст сопернику фигуру с тупыми углами, которая при любом разрезании будет давать острые углы у двух полученных частей.
У второго игрока есть выигрышная стратегия. Он должен своим разрезом каждый раз восстанавливать симметрию фигуры. Например, так:
После второго хода второго игрока получилась фигура (четвёртая), которую как ни разрезай, обязательно получаются две фигуры с острыми углами — второй игрок всегда сможет отрезать от неё один треугольник.
На результат не влияет стратегия первого игрока. Если он отрежет первым ходом меньшую часть, то увеличится общее число ходов, последняя фигура с тупыми углами у второго игрока может получиться другой, но результат будет тот же.
Задача 6. Обозначим массы пяти грузиков, взятые в порядке возрастания: a, b, c, d, e. Всего возможны 6 случаев потери грузика — от самого большого до самого маленького. Запишем значения наших букв для каждого случая и понаблюдаем.
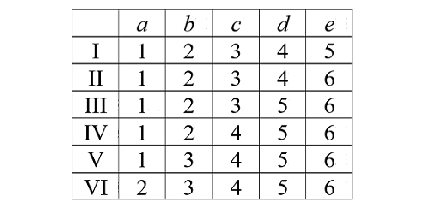
Нужно найти такие равенства с буквами, которые для одних случаев будут верными, для других нет. Это позволит понять, к каким случаям может относиться наш набор грузиков.
Например, равенство a + b + c = e будет верным для случаев II и III и неверным в остальных случаях. Это позволяет провести первое взвешивание: сравнить массы грузиков a + b + c и e. Тем самым мы определим, наши грузики относятся к случаям II и III или к случаям I, IV, V и VI.
Выбирая между II и III случаями, проверим равенство a + c = d. Оно верно для II и неверно для III случая. Здесь хватило двух взвешиваний.
Выбирая между I, IV, V и VI случаями, разобьём их на группы вторым взвешиванием. Проверим равенство a + e = b + d. Оно верно для I и IV и неверно для V и VI случаев. Это было второе взвешивание.
Выбирая между I и IV случаями, проверим равенство a + b = c. Оно верно для I и неверно для IV случая.
Выбирая между V и VI случаями, проверим то же равенство a + b = c. Оно верно для V и неверно для VI случая. Это было третье взвешивание.
Итак, за три взвешивания можно определить, к какому из шести случаев относится данный набор грузиков, то есть за три проверки можно определить, какой грузик потерялся.
Послесловие. Если найдутся более простые способы решения задач, то прошу их прислать. Обсудим. Представляется, что уровень сложности некоторых задач зашкаливает и не соответствует возможностям учащихся 6 класса. А вы как думаете?
Дополнение. Решение задачи 3 исправлено по замечанию Романа Скрябина.
