Новости
Решаем уравнения с отбором корней. ЕГЭ-2024. Профиль

Рассмотрим два задания из сборника [1] для подготовки к ЕГЭ-2024, в которых надо решить комбинированное уравнение (квадратное в совокупности с тригонометрическим или логарифмическим) и отобрать корни.
Косинусы и показательные функции в уравнении с двумя неизвестными
Рассмотрим задачу из белорусского сборника 2013 года для подготовки к их Централизованному тестированию. Она находится в первой части варианта, то есть считается несложной.
Две задачи 25 из ОГЭ-2024. Площади фигур

Рассмотрим решение двух задач на площади фигур из сборника для подготовки к ОГЭ-2024 [1]. Начнём с более простой задачи.
Задача 25 из ОГЭ-2024. Произведение отрезков хорд
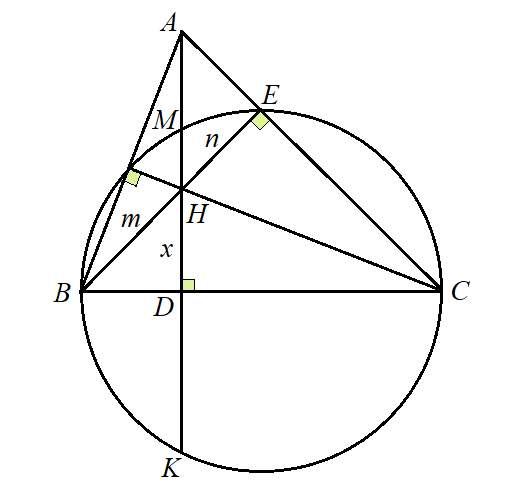
Рассмотрим решение геометрической задачи из сборника [1]. Найти решение в ней не так просто.
Задача 25 из ОГЭ-2024. Три способа решения
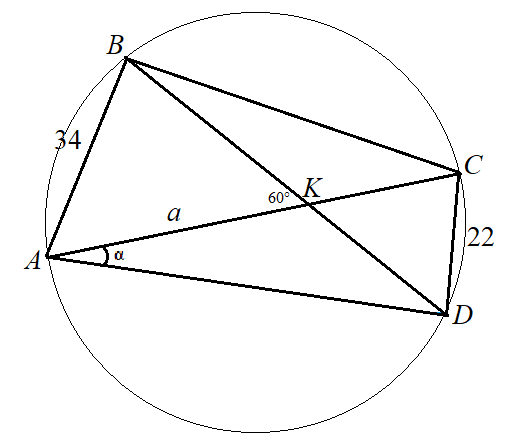
Рассмотрим решение геометрической задачи, в которой могут помешать «лишние» знания: тут можно увидеть пересекающиеся хорды, вписанный четырёхугольник, а потом замучиться применять теоремы, с ними связанные. Мы пойдём другим путём. Итак, задача из сборника [1].
Листая старые книги… Задача с недостающими данными
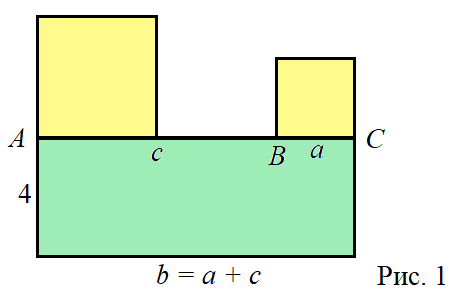
Знакомый учитель математики прислал фото странички из старого пособия [1]. Там есть такая задача.
Докажем рациональность числа

Доказательство рациональности числа с корнями второй степени обычно не так сложны. А вот с корнями третьей и второй степени — немного сложнее. Рассмотрим решение такой задачи.
Не бойтесь вводить «лишние» буквы, или Применяйте подобие треугольников

Рассмотрим задачу по геометрии из сборника «10 вариантов» для подготовки к ОГЭ-2024 [1]. Задача сложная, но имеет простое решение. На её примере покажем ещё раз применение метода, который в шутку можно назвать «Не бойтесь вводить «лишние» буквы».
С Днём рождения книжки!

Сегодня день рождения моей книжки:
Шевкин А. В. Текстовые задачи по математике. 5–6 классы – 3-е изд. перераб. – М. Илекса, 2024. – 160 стр.
ОГЭ-2024 без калькуляторов. Педагогическая общественность отстояла образование

Погоня за ростом показателей математической подготовки школьников при условии, что эта подготовка падает, естественным образом привели Минпрос и Рособрнадзор к решению разрешить на ОГЭ-2024 использовать непрограммируемый калькулятор.
