Не бойтесь вводить лишние буквы, решая задачи по геометрии

Начнём решения задачи, которую, как пишут в Интернете, китайский пятиклассник решил за 2 минуты.
1. Дан параллелограмм ABCD. Точки M и N лежат на сторонах BC и AD соответственно, BM = DN. Площади зелёных многоугольников указаны на рисунке. Найдите площадь розового треугольника.
Решение. На рисунке есть фигуры, площади которых равны. Это Δ ABM и Δ CDN (они равны по…), Δ AMN и Δ CNM (…), четырёхугольники ABMN и CDNM (…).
Здесь есть фигуры, площади которых равны половине площади параллелограмма ABCD. Рассмотрим две такие фигуры: Δ ABL и четырёхугольник CDNM.

Обозначим площади фигур a, b, x — как на рисунке. Так как S_ABK + 79 = 72 + a + b + 8, то S_ABK = a + b + 1 (S_ABK — здесь площадь треугольника ABK). Так как S_ABM =
= S_CDN, то x + a + b + 1 = a + b + 10, откуда x = 9.
Ответ. 9.
2. В прямоугольной трапеции ABCD боковая сторона AB перпендикулярна основаниям BC и AD. Диагонали трапеции пересекаются в точке M. Площадь треугольника MCD равна S. Определите радиус окружности, вписанной в трапецию.
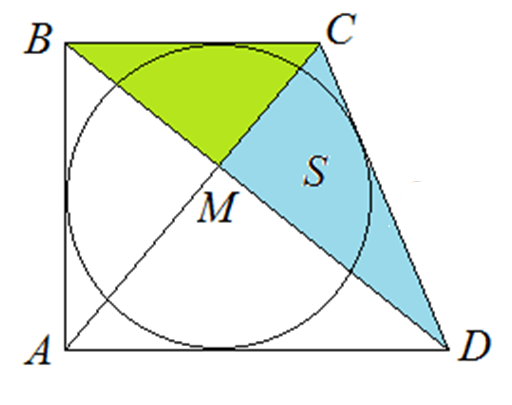
Попробуйте решить задачу самостоятельно. Презентация вам в помощь.
Не бойтесь вводить лишние буквы, решая задачи по геометрии.
В следующей заметке показан другой способ решения задачи 2 и способ быстрого получения ответа в ней.
