Новости
Красивые задачи по геометрии. Площади
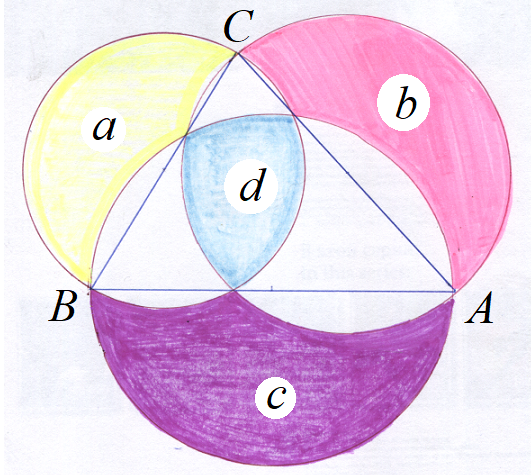
Решим задачу.
Дан остроугольный треугольник, площадь которого равна S. На каждой его стороне, как на диаметре, построили окружность. На рисунке буквами a, b, c, d обозначены площади криволинейных треугольников. Докажите, что 2S = a + b + c – d.
Решение будет опубликовано на сайте www.shevkin.ru, а здесь мы разместим ссылку на него. Предполагается напомнить задачу про луночки Гиппократа и показать, что доказываемое равенство выполняется в прямоугольном треугольнике, в остроугольном (наша задача), в тупоугольном.
А вот и ссылка.
25.01.2020. Красивые задачи по геометрии. Площади. «Луночки» Гиппократа, Равенство 2S = a + b + c — d для площади S треугольника и площадей криволинейных фигур a, b, c, d.
