Физика помогает геометрии
Как только не изображают в сети коронавирус! Видел я шарик с торчащими из него хоботками-присосками. Он напомнил мне многогранник с большим числом граней, к каждой из которых провели перпендикулярный вектор. Задача про такую конфигурацию давно пылится в моём архиве. Она сложно решается средствами стереометрии, но имеет изящное решение при помощи физики.
Эту задачу мне принесли учащиеся 8А физматкласса (старая нумерация классов) в 1983 году. Моё решение они не могли толком понять, так как ещё не изучали стереометрии. Я изложил им только план решения. Зато они привели более простое «физическое» решение, предложенное, как мне сказали, Мишей Смольским. А теперь обо всём по порядку.
Задача. Дан многогранник. От каждой его грани во внешнюю область перпендикулярно плоскости этой грани отложили вектор, длина которого численно равна площади этой грани. Докажите, что сумма всех этих векторов есть нулевой вектор.
Начнём с частного случая, чтобы понять, о чём идёт речь. Рассмотрим куб. Площади всех граней равны. На рисунке показана только одна пара векторов — они противоположны, так как отложены от параллельных граней равной площади, их сумма — нулевой вектор. Сумма трёх таких пар противоположных векторов — нулевой вектор.
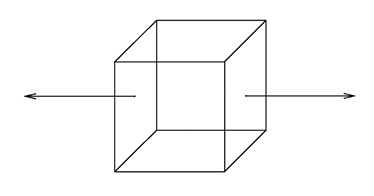
Начнём с частного случая, чтобы понять, о чём идёт речь. Рассмотрим куб. Площади всех граней равны. На рисунке показана только одна пара векторов — они противоположны, так как отложены от параллельных граней равной площади, их сумма — нулевой вектор. Сумма трёх таких пар противоположных векторов — нулевой вектор.
Из-за формул дальше читаем по ссылке.
