«Бесподобная» задача 26 из ОГЭ
Дело вовсе не в том, что задача какая-то особенная. В заметке Сын не справился на пробном ОГЭ с геометрической задачей. Разбираем её дома приведено её решение, к которому у меня нет претензий.
Дело в том, что геометрические задачи полезно решать, привлекая возможно более ранние по времени изучения теоретические факты, тогда эти задачи можно давать учащимся не накануне ОГЭ, а гораздо раньше, что будет способствовать эффективности усвоения материала и разнообразию приёмов решения задач, применяемых школьниками. Итак, задача.
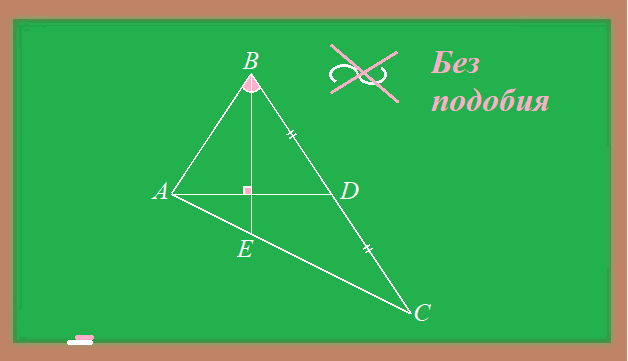
1. В треугольнике АВС биссектриса ВЕ и медиана AD перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника АВС.
Решение. Пусть биссектриса ВЕ и медиана AD пересекаются в точке M. В треугольнике ABD биссектриса BM является высотой, значит, треугольник ABD равнобедренный (AB = BD) и BM является медианой этого треугольника (AM = MD).
Через точку D проведём прямую, параллельную BE. Пусть она пересекает AC в точке N.
Применив теорему Фалеса для угла DAC, получим, что AE = EN.
Применив теорему Фалеса для угла BCA, получим, что EN = NC, то есть AE = EN = NC.
Так как AD = 16, то AM = MD = 8.
В треугольнике BCE отрезок DN является средней линией, DN = 8.
В треугольнике ADN отрезок ME является средней линией, ME = 4.
Тогда BM = 16 – 4 = 12.
Аналогичная задача была в сборнике для подготовки к ОГЭ-2015 (№ 26, вариант 17).
2. В треугольнике АВС биссектриса ВЕ и медиана AD перпендикулярны и имеют одинаковую длину, равную 60. Найдите стороны треугольника АВС.
В презентации рисунок постепенно дополняется, ею удобно пользоваться при объяснении решения учащимся.
