Задача про периметр и площадь прямоугольника
Рассмотрим задачу, предложенную на олимпиаде пятиклассникам в 2018 году и её «взрослое» решение.
2018 5-й класс. Математика. 25 вариантов.
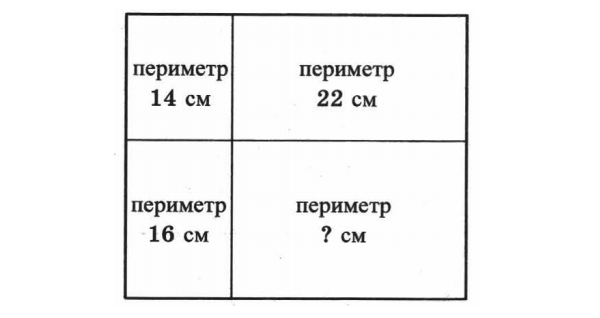
Задание 14. Прямоугольник разбили на четыре маленьких прямоугольника, как показано на рисунке. Периметры трёх маленьких прямоугольников равны 16 см, 14 см и 22 см. Найдите периметр четвёртого маленького прямоугольника. Запишите решение и ответ.
Решение. Обозначим длины сторон прямоугольников как показано на рисунке ниже.
Используя эти обозначения, можно записать равенства:
В задании нужно найти периметр 2x + 2y. Для этого, сложим последние два уравнения, получим:
2a + 2b + 2y + 2x = 16 + 22 = 38,
но 2a + 2b = 14, следовательно,
14 + 2y + 2x = 38,
2y + 2x = 38 – 14,
2y + 2x = 24.
То есть, искомый периметр, равен 24.
Ответ: 24.
Источник. https://self-edu.ru/vpr2018_25.php?id=16_14
Это типичное «взрослое» решение, не учитывающее, что системы линейных уравнений, да такие, где неизвестных (переменных) больше, чем уравнений, сложение уравнений с несколькими неизвестными дети будут изучать только в 7 классе. Ответ должен быть 24 см. А так, задача хорошая, у неё есть и «детское» решение, не требующее знаний из курса алгебры.
2-й способ. Заметим, что два верхних прямоугольника имеют равные высоты (b). Периметр одного прямоугольника больше периметра второго на 22 – 14 = 8 (см), то есть одно основание (x) больше другого (a) на 8 : 2 = 4 (см). Точно такие же основания имеют нижние прямоугольники, у них одно основание (x) больше другого (a) на 4. А периметры отличаются на 2 * 4 = 8 (см). Тогда неизвестный периметр равен 16 + 8 = 24 (см).
Буквы здесь использованы только для того, чтобы показать связь с предыдущим решением. Те же рассуждения можно провести и без букв.
3-й способ. Заметим, что два верхних прямоугольника имеют равные высоты. Периметр одного прямоугольника больше периметра второго на 22 – 14 = 8 (см). Это удвоенная разность оснований прямоугольников. Периметры нижних прямоугольников отличаются тоже на 8, так как у них те же основания. Тогда неизвестный периметр равен 16 + 8 = 24 (см).
Ответ. 24 см.
А теперь приводим ту же олимпиадную задачу (под тем же номером) для шестиклассников (с перестановкой прямоугольников и другим ответом). Пусть учащиеся решат её сами, если им показано решение первой задачи.
Задание 14. Прямоугольник разбили на четыре маленьких прямоугольника, как показано на рисунке. Периметры трёх маленьких прямоугольников равны 14 см, 16 см и 22 см. Найдите периметр четвёртого маленького прямоугольника. Запишите решение и ответ.
А теперь представим, что в задачах речь идёт не о периметрах, а о площадях прямоугольников и 14, 16 и 22 квадратных сантиметра — площади трёх маленьких прямоугольников. Определите площадь четвёртого прямоугольника.
Обе задачи решаются легко — без четырёх букв и уравнений. Разве что неизвестную площадь можно обозначить буквой x и подумать о равных отношениях площадей.
Успехов пяти- и шестиклассникам!
