Выбор метода решения задачи 14. ЕГЭ. Профиль

Неделю назад я писал о выборе способа решения задачи в геометрии.
Не буду спорить про ситуацию на экзамене, но при обучении геометрии мы стараемся учить школьников думать, рассуждать, доказывать, поэтому отклоняем аргументы вроде «подставим числа в формулу, смысла которой не понимаем, и думать не надо» (утрирую). Так мы не выучим функционально грамотных школьников, да и в пространстве они будут плохо видеть.
Итак, я дружелюбно возражаю автору канала «Дружелюбный философ». Вот задача.

Решение задачи методом координат смотрите по ссылке, а мы решим геометрическую задачу геометрически.
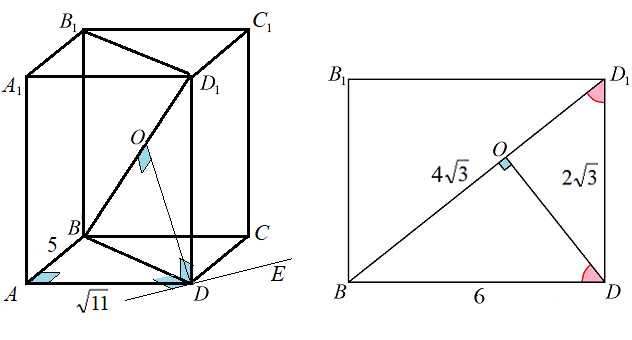

Геометрия не так сложна, чтобы отказываться от её методов в пользу вычислений по формулам.
Дополнение. В личной переписке меня спросили: «А если ученик понимает, что угол между плоскостями — это угол между векторами, перпендикулярными этим плоскостям, если этот угол острый или прямой; или дополняет угол между векторами до развёрнутого, если он тупой?»
Мой ответ
Вам хочется векторов? Их есть у меня! (Помните у Л.О. Утёсова: «Вам хочется песен? Их есть у меня!») Если ученик понимает, что угол между плоскостями в нашей задаче есть острый угол между векторами BB1 и BD1 (между катетом и гипотенузой). Если он толково это объяснит, используя часть выделенного курсивом текста, то пусть сразу переходит в конец первого способа решения, вычисляет длины отрезков и их отношение 0,5, равное косинусу искомого угла.
Если при этом ученик ещё хочет ввести систему координат, и найти длины отрезков по известным формулам, то кто ж ему запретит дольше мучиться?
