Упрощение решения и обобщение одной задачи
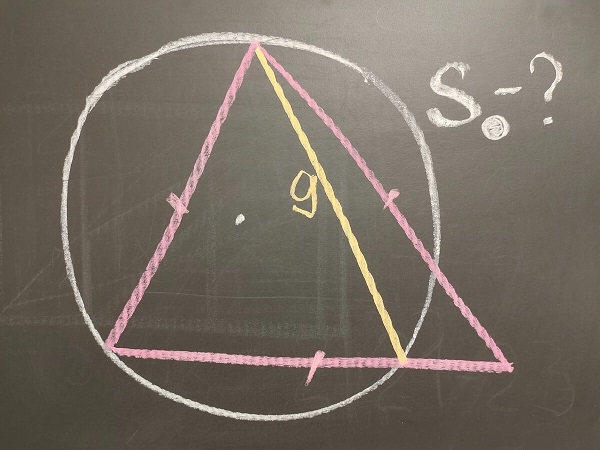
коллега показал, как можно, выполнив дополнительные построения, решить симпатичную задачу. При этом использованы свойства вписанного и центрального углов, теорема Пифагора. Всё это полезно, но для обучения не менее полезно применять и позднее изученные теоремы. Хорошие примеры их применения помогут школьникам полюбить и эти теоремы. Коллега, спасибо за задачу, но я её переформулирую.
1. Окружность, центр которой лежит внутри равностороннего треугольника, проходит через две вершины и пересекает две стороны этого треугольника. Найти площадь круга, если хорда, соединяющая одну вершину треугольника с противолежащей стороной, равна 9.
Попробуем обойтись без дополнительных построений.
В равностороннем треугольнике угол А равен 60 градусов. В треугольнике ABC, вписанном в окружность радиуса R, применим следствие из теоремы синусов, затем найдём R и площадь круга.
Рассмотрите ещё две задачи, меняя условие на центр окружности.
Первый раз пусть центр окружности будет серединой стороны равностороннего треугольника, а второй раз пусть центр окружности лежит вне треугольника. Остальные условия не меняем.
Убедитесь, что и в этих случаях радиус окружности будет тот же. А это означает, что исходная задача содержала лишнее условие — на центр окружности. Переформулируем задачу.
2. Окружность проходит через две вершины и пересекает две стороны равностороннего треугольника. Найдите площадь круга, если хорда, соединяющая одну вершину треугольника с противолежащей стороной, равна 9.
Задача стала сложнее, так как требует рассмотрения трёх случаев и доказательства, что во всех случаях радиус один и тот же.
Коллега, ещё раз спасибо за хорошую задачу.
