Три способа решения одной задачи
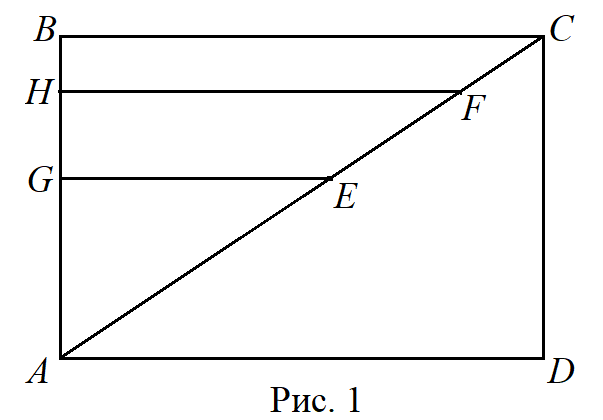
Рассмотрим три способа решения планиметрической задачи, предложенной семиклассникам в конце учебного года.
Для седьмого класса задача трудна, так как требует дополнительных построений. Ребята постарше могут решить её при помощи подобия треугольников и теоремы Пифагора или при помощи тригонометрии.
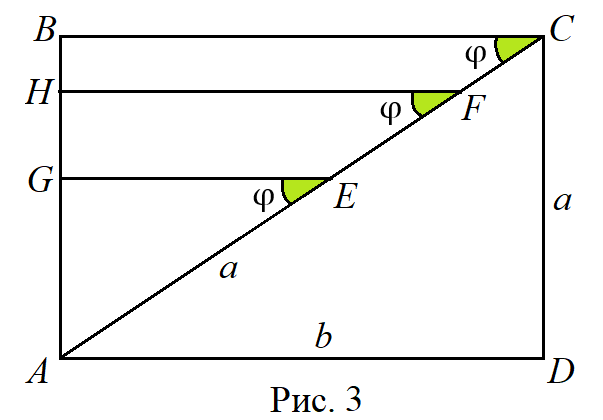
Задача. ABCD — прямоугольник. AE = AB, AF = AD (рис. 1). Докажите, что AG + FH = AC.
Прямоугольные треугольники AEG, ABX и CDY равны по гипотенузе и острому углу (угол A для двух треугольников общий и равен углу третьего треугольника), значит, AG = AX = CY. Из этого следует, что AY = CX.
Прямоугольные треугольники AFH и FAP равны по гипотенузе и острому углу (углы A и F равны как накрест лежащие при параллельных прямых AP и FH и секущей AF). Из этого следует, что AP = FH.
AG + FH = AX + AY = AX + XC = AC, что и требовалось доказать.
Способ 2. Обозначим длины сторон прямоугольника — a и b, величины равных углов BCA, HFA, GEA — φ (рис. 3).