Такого снегопада, такого снегопада…

Как уверяют синоптики, такого снегопада 13 февраля в Москве не было с 1973 года! Эта красота сопряжена с проблемами и трагедиями, а мы обсудим задачи про уборку снега из моего сборника задач для 7-11 классов.
5.84. Через 3 ч после начала снегопада снегоуборочная машина начала уборку снега на участке. Снег продолжал идти. Машина двигалась с постоянной скоростью, сдвигая снег с проезжей части дороги на обочину, и убрала снег на участке за 2 ч. Какая часть выпавшего снега осталась неубранной после окончания работы? Считайте, что процессы выпадения снега и его уборки являются равномерными и что машина убирает снег с любого участка дороги за один заход.
Выясним сначала, какую часть снега, выпадающего за время работы, убирает машина. Для этого представим, что машина начала убирать снег тогда, когда он только начал падать, а закончила работу, когда слой снега составлял а см. Тогда к концу работы в начале участка (и на неубранном участке) лежал слой снега высотой а см.
Так как снегоуборочная машина двигалась равномерно и высота слоя пропорциональна времени снегопада, то слой снега на убранном участке (в разрезе) имеет вид треугольника (рис. 11).
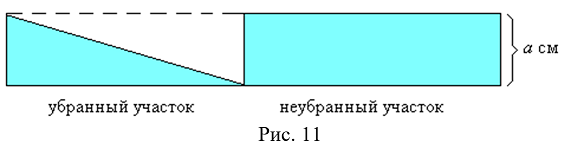
Очевидно, что на убранном участке машина убирает половину снега, выпадающего за время работы. Теперь ответим на вопрос задачи. Если за 3 ч до уборки выпало 3 части снега, то за 2 ч уборки выпало ещё 2 — всего 5 частей снега. Из них осталась неубранной только 1 часть, т. е. 1/5 всего снега, выпавшего за 5 ч.
5.85. Однажды снег шел 6 ч подряд. Он продолжал идти и в следующие 5 ч, за которые снегоуборочная машина убрала участок. Через сколько часов после начала работы машина убрала ровно половину выпавшего к тому времени снега? Считайте процессы выпадения снега и его уборки равномерными.
Пусть машина едет со скоростью v, к началу уборки высота слоя снега составила 6х, где х — высота слоя снега, выпадающего за 1 ч. На рисунке 12 весь участок изображён отрезком АG, а слой снега, выпавшего за 6 ч, изображён прямоугольником АВМG. Пусть через t ч после начала работы будет убрана половина выпавшего к тому моменту снега. Длина участка, убранного за t ч, равна vt, а оставшегося неубранным v(5 – t ).
На рисунке 12 слой снега, выпавшего за t ч, изображен прямоугольником ВNFМ. Его высота равна t х , значит, на неубранном участке высота слоя снега составляет 6х + t х = (6 + t )х.
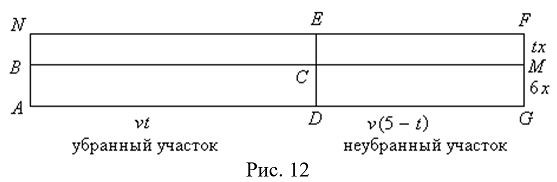
Как мы уже знаем, в любой момент времени оказывается убранной половина снега, выпавшего за время работы машины, следовательно, половина слоя BNEC убрана. Остается определить, когда будет убрано столько снега, выпавшего до начала уборки (ABCD), сколько снега останется на неубранном участке (DEFG),то есть, когда площади прямоугольников ABCD и DEFG окажутся равными. Составим уравнение:
6 xvt = ( t + 6) xv (5 – t ).
Преобразовав полученное уравнение, придём к квадратному уравнению относительно t, имеющему единственный положительный корень t = 3.
Итак, через 3 ч после начала работы будет убрана половина выпавшего к тому моменту снега.
Хорошего вам зимнего настроения!
