Совет против лайфхака
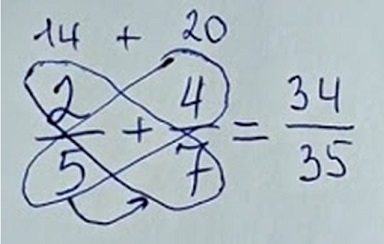
Речь пойдёт о ставшем знаменитым ролике, посвящённом «методу бабочки» для сложения дробей и моему совету, как можно складывать дроби с пониманием того, что мы делаем. Сегодня появилась публикация, которую привожу полностью и комментирую.
В сети признали гениальным простой математический лайфхак
Учитель математики Дмитрий Давидюк опубликовал в TikTok лайфхак, помогающий легко складывать дроби с разными знаменателями, под названием «метод бабочки». В комментариях к его ролику, который за несколько дней набрал 4,5 миллиона просмотров, некоторые пользователи сети признали этот способ гениальным.
Суть «метода бабочки» заключается в том, что при сложении дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой. Сумма двух получившихся чисел будет числителем дроби в ответе, а ее знаменателем — результат умножения знаменателей складываемых дробей.
В комментариях многие поблагодарили математика за предложенный им простой способ. «Если бы так прекрасно учителя объясняли в школе, то я любила бы алгебру», — написала одна из пользовательниц. Некоторые отметили, что благодаря «методу бабочки» наконец-то поняли тему, которая не давалась им в школе, и признали его гениальным.
Ранее учительница из Лондона опубликовала в TikTok видео о популярном в Японии методе умножения двузначных чисел. В комментариях многие поблагодарили ее за помощь, однако часть пользователей сочла ее труд напрасным в эпоху, когда у каждого в телефоне есть калькулятор.
Источник. https://lenta.ru/news/2020/09/10/drobi/
Комментарий. Интернет учит, что лайфхак – это то, что облегчает нашу жизнь, делает её проще, без сложностей и проблем. Нам в России претит обычный совет называть советом, обязательно надо сказать «по-иностранному»? На эту тему вспоминается у Н.В. Гоголя вывеска магазина: «Иностранец Иван Фёдоров». Ну неискоренимо преклонение перед иностранщиной!




Любители лайфхаков могут спросить: а где вы взяли дополнительные множители 3 и 4? Раскладывали знаменатели на простые множители, находили НОК (48; 38) = 144? Я отвечу: нет. Даю мой лайфхак, извините, совет: приложите листок черновика под знаменатели данных дробей, на нём будем писать результаты вычислений.
В этом месте я обычно спрашиваю ребят:
— Знаменатели 48 и 36 взаимно просты?
— Нет, — отвечают они, — оба делятся на 2.
— Отлично, делим оба знаменателя на 2 и результаты подписываем под каждым знаменателем. Получается запись:
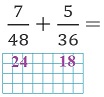
— А теперь числа 24 и 18 взаимно просты?
— Нет, — отвечают они, — оба делятся на 6 (было бы ещё лучше, если бы они сразу заметили, что оба числа 48 и 36 делятся на 12).
— Отлично, делим оба числа 24 и 18 на 6 и результаты подписываем ниже на черновике. Получается запись:
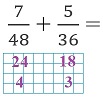
— А теперь числа 4 и 3 взаимно просты? — Не успокаиваюсь я.
— Да, это соседние натуральные числа (любые соседние натуральные числа взаимно просты — такую задачу мы решали по нашему учебнику в 5 классе).
— Числа 4 и 3 являются дополнительными множителями дробей — второй и первой соответственно.
Дальше надо пояснить, что 48 = 12 ∙ 4, 36 = 12∙3, мы за два раза поделили знаменатели на 12, получили 4 и 3. Если первый знаменатель умножить на 3, а второй на 4, то знаменатели станут равными, вот почему мы числитель и знаменатель первой дроби умножили на 3, а второй дроби — на 4. Наш способ позволяет привести дроби к общему знаменателю.
Вот и весь секрет моего совета. Было бы интересно узнать мнение Дмитрия Давидюка по поводу моего совета. А ещё спросить о том, как надо учить детей: показывать им, как получить верный результат, или делать это так, чтобы дети понимали, почему он верный.
