Сколько решений имеет задача? (Класс 5+)
На днях встретил в Интернете заметку про задачу, подобные которым решал и составлял больше полугода тому назад: Исследовательские задачи для школьников (класс 5+) .
Автор заметки сформулировал старую олимпиадную задачу и нашёл одно её решение. Привожу условие задачи с небольшим редактированием.
1. На сторонах треугольника находятся кружки — по одному в каждой вершине треугольника и по два на каждой стороне. Надо расставить в эти кружки числа от 1 до 9 без повторения так, чтобы сумма четырёх чисел на каждой из сторон равнялась 17.
Задачка из СССР оказалась не простой. Потребовалось несколько попыток, чтобы решить её правильно.
Автор заметки привёл одно решение, не объяснив, почему в угловых кружках стоят числа 1, 2, 3 и могут ли стоять другие. Восполним этот пробел и выясним, сколько различных решений имеет эта задача.
Итак, сумма всех девяти чисел в кружках равна 1 + 2 + … + 9 = 45. А сумма трёх четвёрок чисел на сторонах треугольника равна 3 * 17 = 51 — она на 6 больше, так как числа, стоящие в угловых кружках посчитаны дважды. Сумма этих трёх чисел равна 51 – 45 = 6. Имеется единственная возможность получить такую сумму: 1 + 2 + 3 = 6.
Три угловых числа поставим в порядке возрастания от верхней вершины треугольника при обходе вершин треугольника по часовой стрелке. Около каждой стороны напишем все возможные суммы, которые с угловыми числами дают 17.
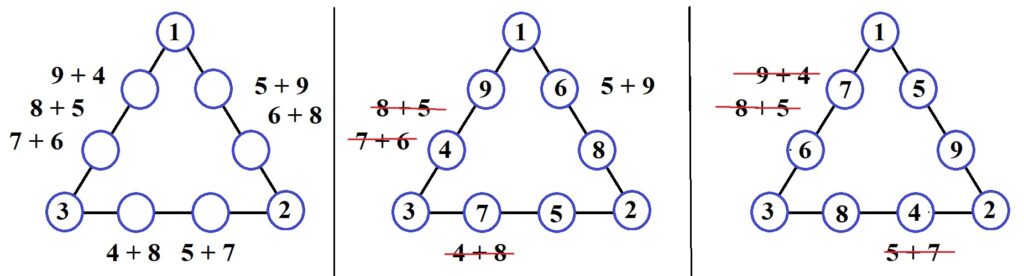
Пробуем поставить на одной стороне числа 6 и 8, на других сторонах вычеркнем суммы с числами 6 или 8. Оставшиеся числа впишем в кружки, соблюдая правило: при движении по часовой стрелке на стороне треугольника сначала ставим меньшее число, потом большее.
Затем поставим на одной стороне числа 5 и 9, на других сторонах вычеркнем суммы с числами 5 или 9. Оставшиеся числа впишем в кружки по тому же правилу.
Наши решения можно записать в виде девятизначных чисел, если прочитать написанные числа от верхней вершины по часовой стрелке: 159248367 и 168257349. Других решений данная задача не имеет, а правило чтения решения нужно для того, чтобы не считать новым решение, полученное из наших двух перестановкой чисел на стороне треугольника, поворотом или симметрией треугольника.
2. На каждой стороне того же треугольника надо расставить в кружки числа от 1 до 9 без повторения так, чтобы сумма четырёх чисел на каждой из сторон равнялась 18. Имеет ли эта задача решение?
3. На каждой стороне того же треугольника надо расставить в кружки числа от 1 до 9 без повторения так, чтобы сумма четырёх чисел на каждой из сторон равнялась 19. Сколько решений имеет эта задача?
