Решайте задачи проще!
Рассмотрим три задачи, разбор решений которых можно найти на одном из каналов Валерия Волкова. Хвалю его за большую работу, подробный и понятный разбор решений, но иногда обнаруживаю, что он не показывает самые простые способы решения задач.
Задача 1. Решите уравнение: |x – 2| = |x + 5|.
Рассмотрим заключительный кадр видео, на котором приведены два способа решения уравнения. Первый симпатичный, но он не имеет общего характера. При разных коэффициентах при x он не работает, например, для уравнения |3x – 2| = |x + 5|.
Второй способ хорош, он универсален.
Но здесь нет третьего способа, основанного на том, что модули двух чисел равны тогда и только тогда, когда числа равны или противоположны.
Решение. Найдём такие числа x, для каждого из которых:
1) x – 2 = x + 5 или 2) x– 2 = – (x + 5).
Уравнение 1) не имеет корня, уравнение 2) имеет один корень –1,5.
Это число и является корнем исходного уравнения.
Задача 2. Квадрат разделили на два прямоугольника. Найдите сторону квадрата, если периметры полученных прямоугольников 13 и 17.
На видео приведён способ решения, требующий введения двух букв. Вот последний кадр решения, из которого всё понятно.
Между тем, можно было обойтись одной буквой и решать задачу со школьниками, которые ещё не умеют решать систем линейных уравнений.
Решение. Обозначим сторону квадрата x. Тогда сумма двух периметров равна 6x, чтобы в этом убедиться, воспользуемся первым кадром видео. Покрасим стороны прямоугольников двумя цветами, как показано на рисунке. Стороны квадрата оказались закрашенными, хотя бы в один цвет по одному разу, а отрезок внутри квадрата закрашен дважды, то есть в сумме периметров 17 + 13 отрезок длины x содержится 6 раз.
Итак, решив уравнение 6x = 17 + 13, получим его единственный корень 5. Это и есть сторона квадрата.
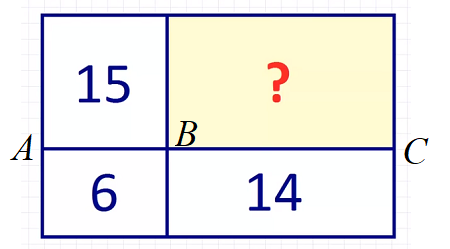
Задача 3. Прямоугольник разделили на четыре меньших четырёхугольника прямыми, параллельными его сторонам. Площади трёх маленьких прямоугольников, как показано на рисунке, равны 15, 6 и 14. Найдите площадь четвёртого прямоугольника.
Для решения задачи введены четыре буквы. По ходу решения сделано замечание, что для решения таких задач «по-быстрому» надо перемножить числа по диагонали:
6x = 15 ∙ 14.
Это всё неплохо, но давайте вернёмся к первому кадру.
Отношение площадей прямоугольников, имеющих равные стороны, равно отношению других сторон этих прямоугольников. В самом деле, если стороны одного прямоугольника a и b, а второго — a и c, то отношение площадей равно ab : ac = b : c.
В нашей задаче отношение отрезков AB : BC равно 6 : 14 или 15 : x, где x — неизвестная площадь прямоугольника.
Решив пропорцию
6 : 14 = 15 : x,
6x = 15 ∙ 14,
получим x = 35.
Итак, площадь четвёртого прямоугольника равна 35.
В ходе решения пропорции у нас получилось упомянутое выше равенство для решения таких задач «по-быстрому». Только учащимся для понимания решения гораздо полезнее приравнивать две пары отношений и решать пропорцию.
Ссылка на статью: Решайте задачи проще
