Решаем задачу проще
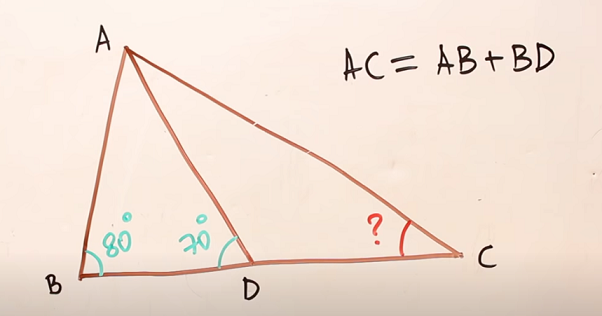
По ссылке, приведённой ниже, можно посмотреть ролик с решением задачи, условия которой понятны из рисунка. Вот эта задача.
1. В треугольнике ABC угол B равен 80 градусам. На стороне BC отметили точку D так, что угол ADB равен 70 градусам и AC = AB + BD. Найдите угол C.
Источник. https://youtu.be/kS-Pq_rJrjs
В ролике приведено решение с применением четвёртого признака равенства треугольников. Мы обойдёмся без него, а потом рассмотрим ещё более простой способ решения задачи. Итак, решение, которое мы обсуждаем, предлагает «спрямить» сумму двух отрезков, отложив на луче AB за точку B отрезок BE, равный отрезку BD. Соединим точки В и D.
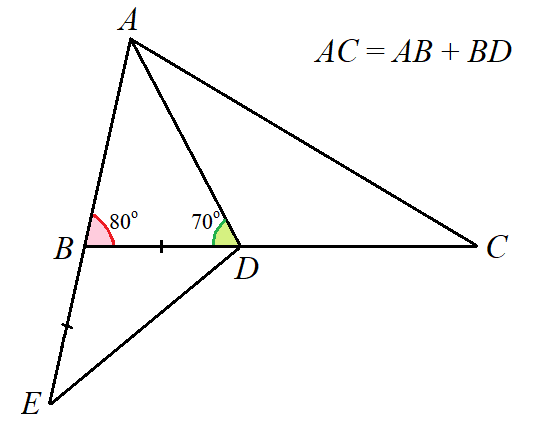
Так как угол ABD внешний для треугольника BDE, то он равен сумме двух равных углов при основании равнобедренного треугольника, следовательно, углы E и D в треугольнике BDE равны 40 градусам. Тогда угол ADE равен углу ADC и равен 110 градусам.
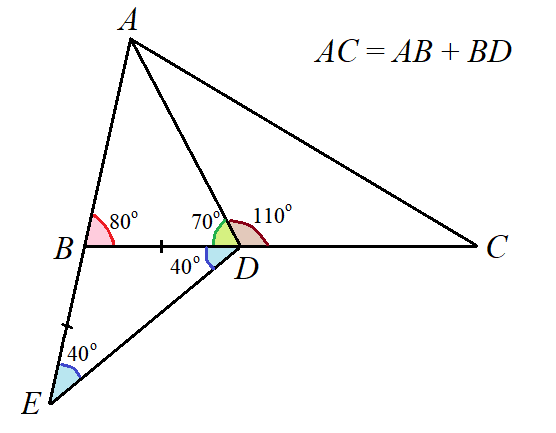
В треугольниках ADE и ADC стороны AE и AС равны, сторона AD — общая, углы ADE и ADC равны. Докажем от противного, что DE = DC.
Предположим, что DE < DC. Отметим точку M на отрезке DC так, что DM = DE и соединим точки A и M.
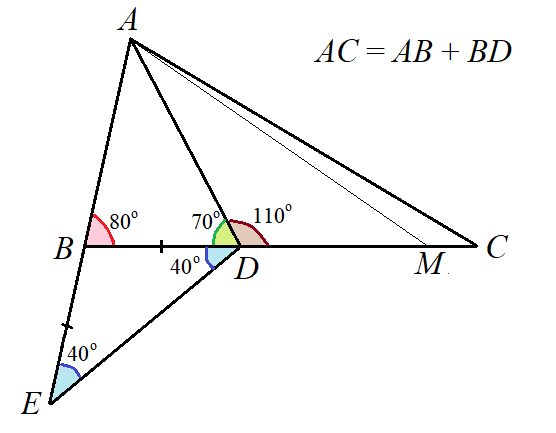
Из нашего предположения следует, что треугольники ADE и ADM равны по двум сторонам и углу между ними. Тогда AM = AC и угол AMD равен 40 градусам, но это невозможно, так как в равнобедренном треугольнике AMC окажется два тупых угла по 140 градусов.
Следовательно, наше предположение, что DE < DC неверно (в случае
DE > DC доказательство аналогично) и DE = DC. Тогда треугольники ADE и ADC равны по двум сторонам и углу между ними и искомый угол C равен 40 градусам.
Рассмотрим второй способ решения. «Спрямим» сумму отрезков AB и BD иначе. Отложим на луче DB за точку B отрезок BN, равный отрезку AB. Соединим точки A и N.
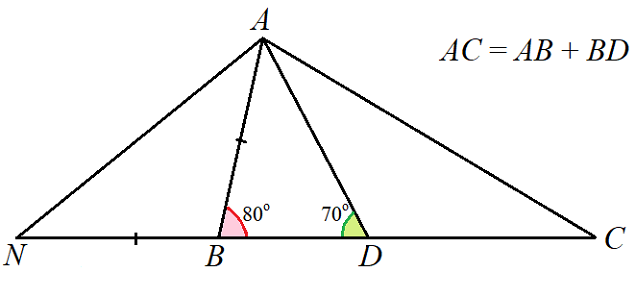
В треугольнике ABD угол A равен 30 градусам, а в треугольнике ABN углы A и N равны по 40 градусов.
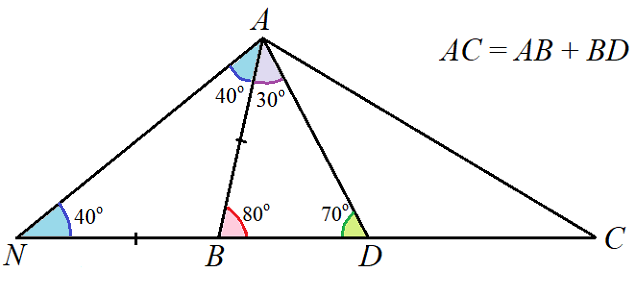
Тогда угол DAN равен углу ADN и ND = AN, но ND = AB + BD = AC. Значит, AN = AC и угол C равен углу N, и равен 40 градусам.
Ответ. 40 градусов.
