Расставим числа на окружности
В хорошей школе используют специальную форму работы — листки с задачами олимпиадного уровня. Такие листки мне тоже доводилось использовать, поэтому стало интересно, что теперь дают решать на листках шестиклассникам. Итак, задача.
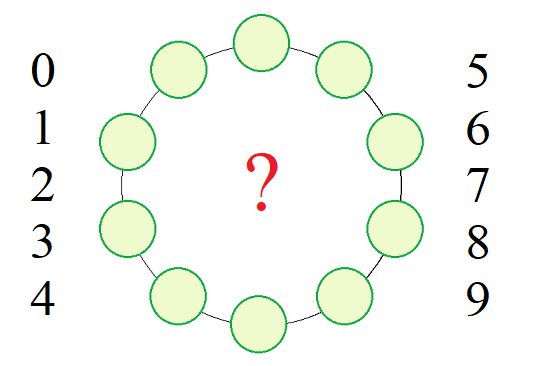
1. Можно ли на окружности расположить числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы любые два соседние числа отличались на 3, 4 или 5?
Простота формулировки задачи подкупает, но попытки осуществить требуемое наводят на мысль: «А можно ли осуществить требуемое?» Гипотеза «это невозможно осуществить» требует доказательства.
Расположим данные числа в трёх строках, как показано на рисунке.
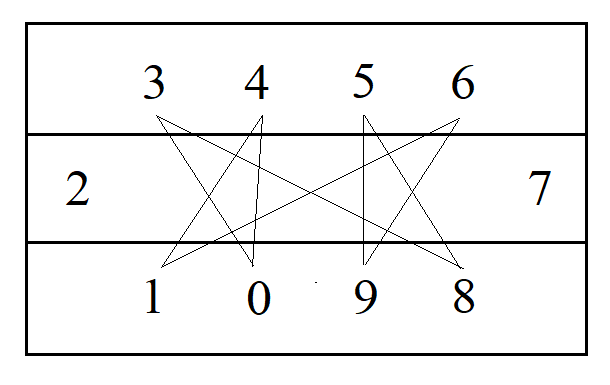
Числа из нижней строки не имеют соседей ни в своей, ни в средней строке — все их возможные соседи стоят в верхней строке.
Предположим, что мы расположили числа на окружности согласно условиям задачи, тогда у чисел из нижней строки будет по два соседа из верхней строки. На рисунке показан один из вариантов установления соседства: числа-соседи соединены тонкими линиями. Но тогда у чисел из верхней строки соседи могут быть только в нижней строке, поэтому у чисел 2 и 7 не будет соседей из верхней строки, что невозможно.
Наше предположение, что можно расположить числа на окружности согласно условиям задачи, неверно. Следовательно, расположить числа на окружности согласно условиям задачи невозможно.
Задача для самостоятельного решения
2. а) Можно ли на окружности расположить числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы любые два соседние числа отличались на 4, 5 или 6?
б) Если задание а) можно выполнить, то сколько существует различных расположений чисел на окружности?
А.В. Шевкин, avshevkin@mail.ru.
