ЕГЭ-2022 по математике. Комплексные числа

Продолжаем обсуждать документ ФИПИ с длинным названием Перспективная модель измерительных материалов для государственной итоговой аттестации по программам среднего общего образования по МАТЕМАТИКЕ. Демонстрационный вариант
Перспективные модели (fipi.ru)
Сегодня поговорим о содержании, которого до сих пор никогда не было в ЕГЭ, но всегда присутствовало в выпускном экзамене по программе углубленного изучения математики. На мой взгляд, это ошибка составителей варианта. Нельзя устраивать дискриминацию учащихся, не изучавших математику углублённо. Рассмотрим задачу.

Ученику обычного класса придётся прочитать про комплексные числа, про мнимую единицу i, квадрат которой равен –1. Про то, что комплексным числом называют выражение z, записанное в виде z= a + bi, где a и b— действительные числа, а i — мнимая единица. Комплексное число задаётся парой действительных чисел (a; b), его удобно изображать в системе координат точкой (a; b). Модулем комплексного числа называют расстояние от начала отсчёта системы координат до точки, изображающей число z. Модуль комплексного числа z= a + bi вычисляют по формуле:

Ответ. 2,4.
Решим задачу, изображая комплексное число точкой координатной плоскости. Этот способ вполне годится для решения задачи на ЕГЭ, так как там подробное решение не требуется, достаточно привести правильный ответ. Изобразим на клетчатой бумаге точками числа

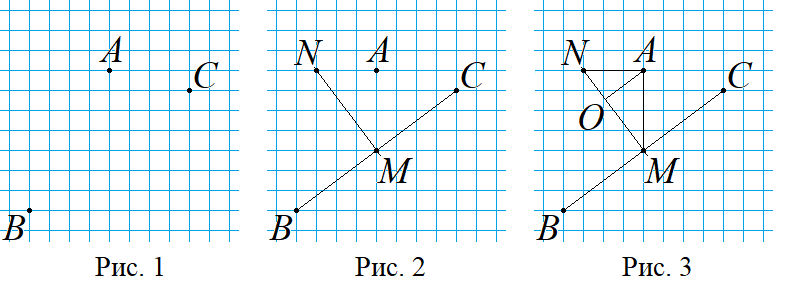
Точка O лежит на прямой MN, а нам требуется, чтобы расстояние AO было наименьшим, это возможно лишь тогда, когда является перпендикуляром к AO. Строим AO и находим его длину как высоту прямоугольного треугольника AMNс гипотенузой MN (рис 3).
Вычислив площадь треугольника AMN двумя способами, выразим длину высоты, проведённой к гипотенузе MN. Получим 2,4.
Скачать статью: ЕГЭ 2022 Вероятность и комплексные числа
Дополнение от 26.12.2020. После публикации вчерашних новостей про ГВЭ стало понятно, что ЕГЭ уже в 2021 году будет одного уровня, поэтому слов «профильный уровень» в текстах о ЕГЭ 2022 года нет. Что такое ГВЭ поговорим чуть позже.
