Пришёл, увидел, решил! Чёрно-белые разности
Поводом для данной заметки послужила задача, которую мы разберём в конце, а пока рассмотрим шуточную «теорию чёрно-белых разностей».
Пусть дана фигура, разбитая линиями на части и раскрашенная «в шахматном порядке» в чёрный и белый цвет.
Определение 1. Чёрно-белой разностью периметров данной фигуры (обозначение: RP) назовём разность суммы периметров всех чёрных частей этой фигуры и суммы периметров всех белых её частей.
Определение 2. Чёрно-белой разностью площадей данной фигуры (обозначение: RS) назовём разность суммы площадей всех чёрных частей этой фигуры и суммы площадей всех белых её частей.
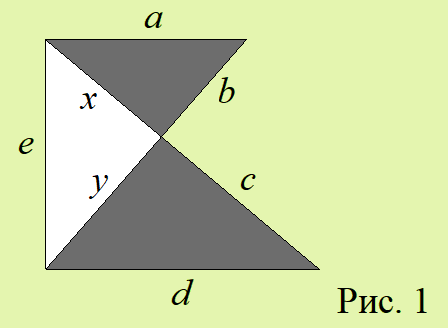
Чёрно-белая разность периметров фигуры зависит только от длин линий, составляющих границу данной фигуры. Покажем это на простом примере (рис. 1).
RP = (a + b + x + c + d + y) – (e + x + y) = a + b + c + d – e.
Другими словами, все длины границ между чёрными и белыми частями фигуры при вычитании компенсируют друг друга, они не влияют на величину RP.
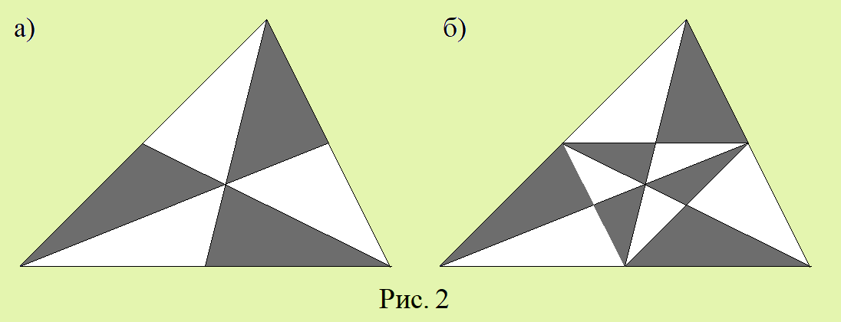
1. Докажите, что для треугольника (рис. 2) RP = 0 и RS = 0, если: а) провели три медианы; б) провели три медианы и три средние линии треугольника.
2. Докажите, что для треугольника (рис. 3), RP = 0, если: а) центр окружности, вписанной в треугольник, соединили с вершинами треугольника и с точками касания этой окружности со сторонами треугольника; б) провели три биссектрисы углов треугольника до пересечения с окружностью, описанной около этого треугольника; в) провели три серединных перпендикуляра к сторонам треугольника и точку их пересечения соединили с вершинами треугольника.
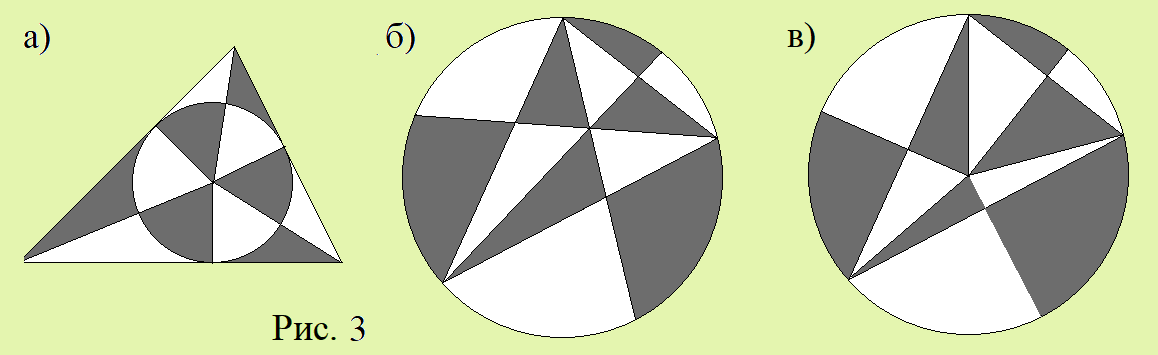
3. Определите, в каких из трёх случаев (рис. 3, а, б, в) RS = 0.
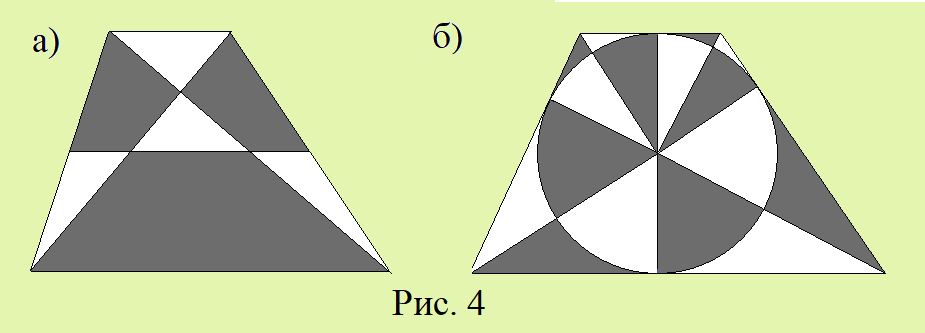
4. В трапеции с основаниями a и b (a > b) провели среднюю линию и диагонали (рис. 4, а). Докажите, что RP = a – b.
5. В трапецию вписана окружность. Её центр соединили с вершинами трапеции и с точками касания окружности со сторонами трапеции (рис. 4, б). Докажите, что RP = 0 и RS = 0.
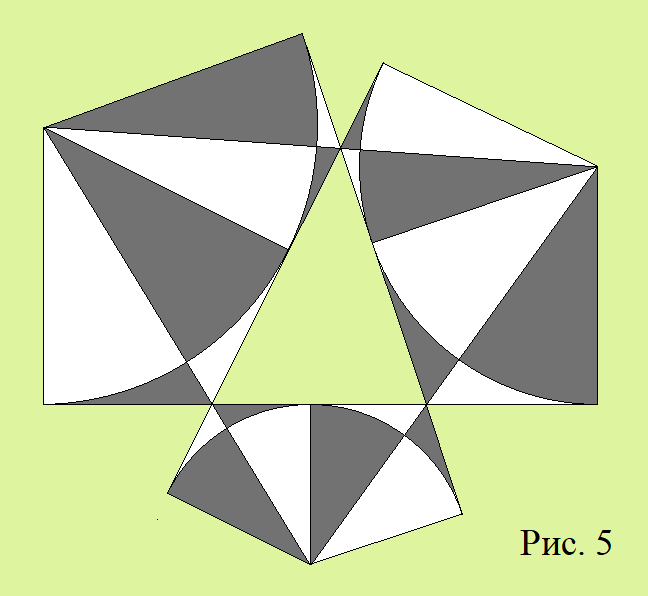
6. К треугольнику (зелёный на рис. 5) провели три вневписанные окружности, центры которых соединили с точками касания прямых, содержащих стороны треугольника, а также с двумя ближайшими вершинами треугольника. Докажите, что RP = 0 и RS = 0.
7. На сторонах треугольника ABC отметили точки M, N и K. Периметры получившихся треугольников равны a, b, c и d (см. рис. 6). Выразите периметр треугольника ABC через a, b, c и d.
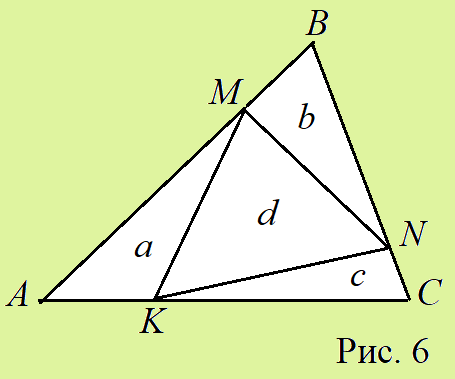
Даже не закрашивая треугольники, можно догадаться, что для вычисления периметра треугольника ABC надо сложить периметры a, b и c, но в этой сумме будут лишними длины отрезков MN, NK и MK, составляющие в сумме d. Искомый периметр a + b + c – d.
А завершим нашу заметку задачей, предложенной пятиклассникам на Малом мехмате МГУ. Она и породила цепочку задач, приведённых выше.
8. Треугольное стекло разбилось на 57 треугольных кусочков, как показано на рис. 7. Если Жене, разбившему стекло, указать на любой кусочек, то он назовёт периметр этого кусочка. Как узнать периметр первоначального куска стекла?
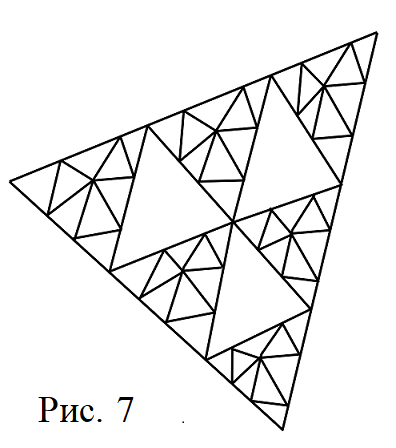
Заметим, что стороны большого треугольника не разделены на три равные части, треугольники, занимающие одинаковые места внутри треугольников среднего размера, не равны между собой. Так как стекло разбилось на 57 белых осколков, то задача не решается, если не положить каждый осколок на своё место.
Представим, что мы догадались раскрасить треугольник «в шахматном порядке» до того, как Женя разбил стекло, тогда у нас есть шанс определить периметр самого большого треугольника. Сколько вопросов пришлось бы задать Жене для получения ответа в задаче?
P. S. Выражаю благодарность Нестерской Маше, приславшей ссылку на материалы Малого мехмата МГУ с задачей 8.