Планиметрия. Задача на площади
Рассмотрим две задачи на определение отношения площадей фигур.
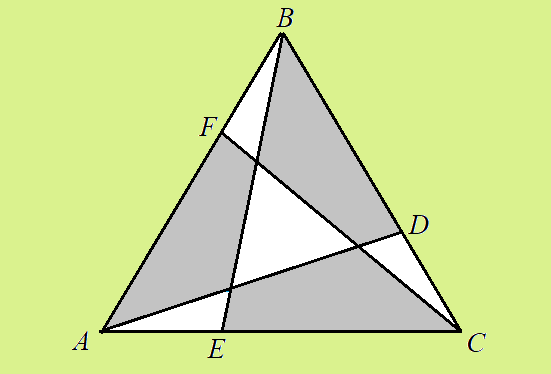
1. В равностороннем треугольнике ABC стороны AB, BC и CA разделены точками F, D и E в отношении 2 : 1. Отрезки AD, BE и CF разделили треугольник ABC на семь многоугольников (рис. 1). Многоугольники покрасили в шахматном порядке в серый и в белый цвет. Найдите отношение площади серой части треугольника ABC к площади его белой части.
Рис. 1
Рис. 2
Из равенства площадей треугольников ABE, BCF и CAD— площадь каждого составляет треть площади треугольника ABC — следует, что сумма площадей этих треугольников равна площади треугольника ABC. Эта сумма включает лишнюю сумму 3x и не включает площадь большого белого треугольника. Следовательно, площадь большого белого треугольника равна 3x.
Так как отношение площадей треугольников с общей вершиной и основаниями, лежащими на одной прямой, равны отношению длин оснований, то y: x = (3x + y) : 2x, откуда следует, что y = 3x.
Теперь найдём искомое отношение площади серой части треугольника ABC (С) к площади его белой части (Б):
С : Б = 3(2x + y) : 6x = 15x : 6x = 5 : 2.
Ответ. 5 : 2.
Заметим, что установленное свойство площадей имеет место и для произвольного треугольника. Докажем его более простым способом, который можно назвать способом введения дополнительных неизвестных, или способом введения «лишних» букв.
2. В треугольнике ABC стороны AB, BC и CA разделены точками F, D и E в отношении 2 : 1. Отрезки AD, BE и CF разделили треугольник ABC на семь многоугольников (рис. 3). Многоугольники покрасили в шахматном порядке в серый и в белый цвет. Найдите отношение площади серой части треугольника ABC к площади его белой части.
Рис. 3
Решение. Соединим вершины большого белого треугольника с вершинами треугольника ABC как показано на рис. 4.
Рис. 4
Обозначим площади треугольников буквами: x, y, z — площади малых белых треугольников, 2x, 2y, 2z — площади малых серых треугольников, a, b, c — площади больших серых треугольников.
Из равенства площадей треугольников ABE, BCF и CAD — площадь каждого составляет треть площади треугольника ABC — следует, что сумма площадей этих треугольников равна площади треугольника ABC. Эта сумма включает лишнюю сумму x + y + z и не включает площадь большого белого треугольника. Следовательно, площадь большого белого треугольника равна x + y + z.
Так как отношение площадей треугольников с общей вершиной и основаниями, лежащими на одной прямой, равны отношению длин оснований, то верно равенство (x + y + z + c) : 2x = a : x, откуда следует, что
x + y + z + c = 2a. (1)
Аналогично получим ещё два равенства:
x + y + z + b = 2c, (2)
x + y + z + a = 2b. (3)
Сложив равенства (1), (2), (3), после преобразования получим:
3(x+ y + z) = a + b + с.
Теперь найдём искомое отношение площади серой части треугольника ABC (С) к площадей его белой части (Б).
С : Б = (2x + 2y + 2z + a + b + с) : (2x + 2y + 2z) =
= (5x + 5y + 5z) : (2x + 2y + 2z) = 5 : 2.
Ответ. 5 : 2.
Мы обошлись без доказательства фактов, что x = y = z и что a = b = с. Эти доказательства являются хорошей тренировкой для любителей планиметрии. Рассмотрим ещё один способ решения задачи 2 с применением теоремы Фалеса.
Решение. Разделим отрезок AB на 6 равных частей и через точки деления проведём прямые, параллельные прямой AD. Отрезок CF разделится в отношении CK : KF = 3 : 4 (рис. 5).
Разделим отрезок AC на 9 равных частей и через точки деления проведём прямые, параллельные прямой BE. Отрезок CF разделится в отношении CN : NF = 6 : 1 (рис. 6).
Таким образом, точки K и N разделили отрезок CF в отношении
CK : KN : NF = 3 : 3 : 1 (рис. 3).
Скачать статью: Планиметрия. Площади
