Олимпиадная задача про драконов для шестиклассников

14 октября я поместил олимпиадная задачу для пятиклассников на двух сайтах. Обычная реакция на задачи по математике слабенькая, а тут взрыв интереса.
Олимпиадная задача для пятиклассников… и ещё две задачи | Наблюдатель |
Я уже подготовил заметку Логические задачи — от простой задачи к сложным, а сегодня получил олимпиадную задачу для шестиклассников. Начнём с неё, а потом посмотрим более сложные задачи с решениями.
1. В стране Драконии живут красные, зеленые и синие драконы. У каждого дракона три головы, каждая из которых всегда говорит только правду или всегда лжет. При этом у каждого дракона хотя бы одна голова говорит правду. Однажды за круглый стол сели 590 драконов, и каждый из них сказал:
1) 1-я голова: «Слева от меня сидит зеленый дракон».
2) 2-я голова: «Справа от меня сидит синий дракон».
3) 3-я голова: «Рядом со мной нет красного дракона».
Какое наибольшее количество красных драконов могло быть за столом?
Первое впечатление: не решить! Мы же не знаем, какая голова у какого дракона что говорит, всех вариантов и не перебрать. Но не будем торопиться. Просят указать наибольшее возможное число красных драконов. По доброте душевной мы бы указали 590 — и делу конец, но возможно ли это? Начнём с малого.
Может ли с драконом любого цвета (?) быть рядом два красных дракона (К) (рис. 1)? Оказывается нет, так как у дракона (?) ни одна голова не сможет сказать правды, что противоречит условию задачи.
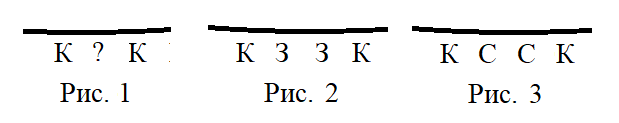
Могут ли между двумя красными драконами сидеть два дракона других цветов и в каком порядке? Рассмотрим все возможные случаи (рис. 2-5).
Из двух драконов зелёного цвета (рис. 2) спросим того, что левее. Вот его ответы.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — Л.
2) 2-я голова: «Справа от меня сидит синий дракон» — Л.
3) 3-я голова: «Рядом со мной нет красного дракона» — Л.
Этот случай невозможен.
Из двух драконов синего цвета (рис. 3) спросим того, что правее. Вот его ответы.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — Л.
2) 2-я голова: «Справа от меня сидит синий дракон» — Л.
3) 3-я голова: «Рядом со мной нет красного дракона» — Л.
Возможен ли случай, изображенный на рисунке 4?
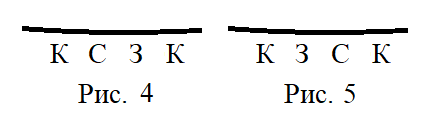
Вот ответы синего дракона.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — Л.
2) 2-я голова: «Справа от меня сидит синий дракон» — Л.
3) 3-я голова: «Рядом со мной нет красного дракона» — Л.
Такой случай (рис. 4) рассадки невозможен.
Возможен ли случай, изображенный на рисунке 5? Вот ответы зелёного дракона.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — Л.
2) 2-я голова: «Справа от меня сидит синий дракон» — Истина (И).
3) 3-я голова: «Рядом со мной нет красного дракона» — Л.
А это ответы синего дракона.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — И.
2) 2-я голова: «Справа от меня сидит синий дракон» — Л.
3) 3-я голова: «Рядом со мной нет красного дракона» — Л.
Такой случай рассадки (рис. 5) возможен, и он единственный для зелёного и синего драконов! Мы ищем наибольшее число красных драконов, поэтому увеличивать число зелёных и синих драконов между красными не будем. Выясним, можно ли соединить две такие цепочки, как на рисунке 5?
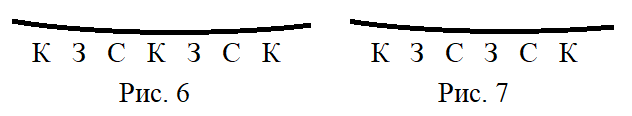
Спросим у красного дракона, оказавшегося посередине (рис. 6).
Его ответы.
1) 1-я голова: «Слева от меня сидит зеленый дракон» — Л.
2) 2-я голова: «Справа от меня сидит синий дракон» — Л.
3) 3-я голова: «Рядом со мной нет красного дракона» — И.
Итак, цепочку драконов при найденной рассадке можно наращивать.
Если бы у нас было 588 драконов, то мы соединили бы 196 троек К — З — С — по кругу и наибольшее число красных драконов было бы 196 (по одному в каждой тройке). Нам осталось посадить ещё двух драконов, чтобы всего их было 590. Добавить красного дракона нельзя, добавим синего и зелёного цвета. Такая рассадка существует (рис. 7). Проверкой убеждаемся, что у каждого синего и у каждого зелёного дракона найдётся голова, говорящая правду (проверьте).
Итак, наибольшее число красных драконов 196.
Ответ. 196.
