Олимпиадная задача для девятиклассников
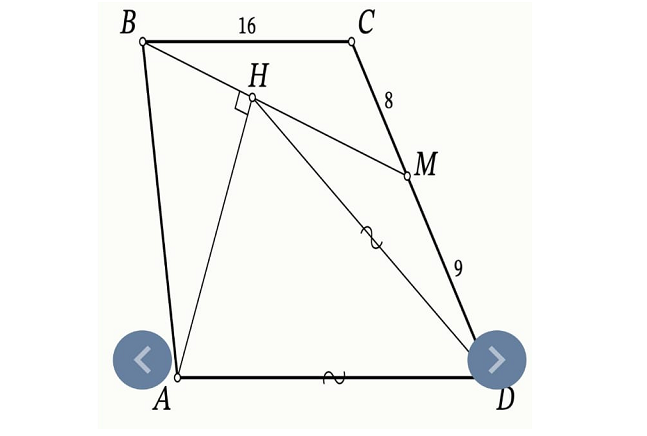
В комментарии к решению олимпиадных задач мне прислали фото с задачей, снятой на телефон ученика 9 класса. Фото на заставке к новости. А вот и текст задачи.
1. На боковой стороне CD трапеции АВСD (АD || ВС) отмечена точка М. Из вершины А на отрезок ВМ опущен перпендикуляр АН. Оказалось, что АD = НD. Найдите длину отрезка АD, если известно, что ВС = 16, СМ = 8, МD = 9.
Давайте на примере этой задачи поучим ребят искать решение задач, пользуясь теми подсказками, которые есть в условиях задачи.
1) Проведём медиану DF к основанию равнобедренного треугольника ADH, она является высотой.
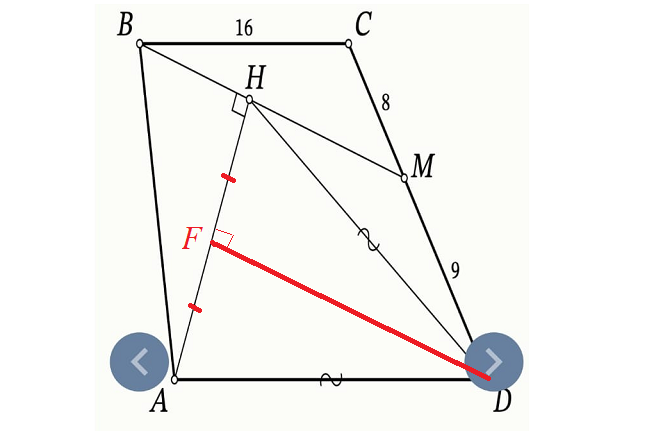
2) Из перпендикулярности DF и BM одной прямой следует, что DF || BM. Эти параллельные прямые пересекают прямую CD, отсекая на ней отрезки 8 и 9, но пока нет условий применить теорему о пропорциональных отрезках — не хватает второй прямой.
3) Проведём прямую, перпендикулярную BM через точку C, она пересечёт BM и DF в точках P и S соответственно.
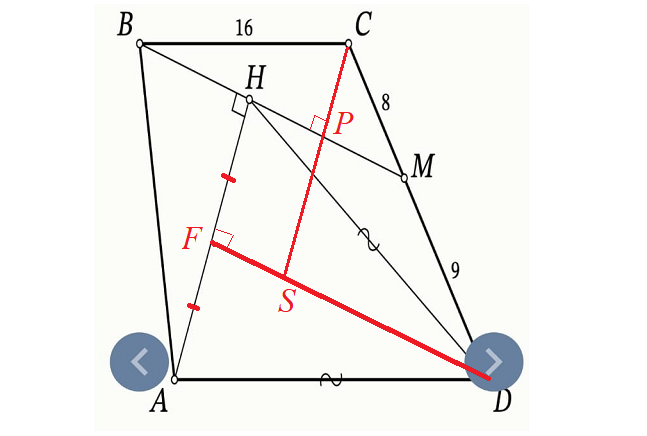
Теперь по теореме о пропорциональных отрезках имеем: CP : PS = 8 : 9. Обозначим CP = 8x, PS = 9x. Тогда в прямоугольнике HPSF HF = 9x, а в равнобедренном треугольнике ADH AF = 9x.
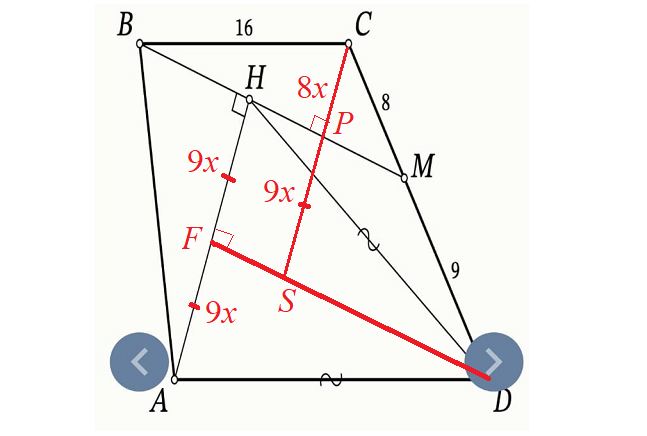
Вернёмся к вопросу задачи и посмотрим, все ли данные из условия задачи мы использовали. Нас просят найти AD — гипотенузу прямоугольного треугольника ADF, а не использовали мы пока что тот факт, что BC = 16, а это гипотенуза прямоугольного треугольника CBP.
4) В прямоугольных треугольниках ADF и CBP углы ADF и CBP, равны, так как их стороны — противоположно направленные лучи. Треугольники подобны по двум углам и из пропорции AD : BС = AF : СP получаем: AD : 16 = 9 : 8, откуда AD = 18.
Ответ. 18.
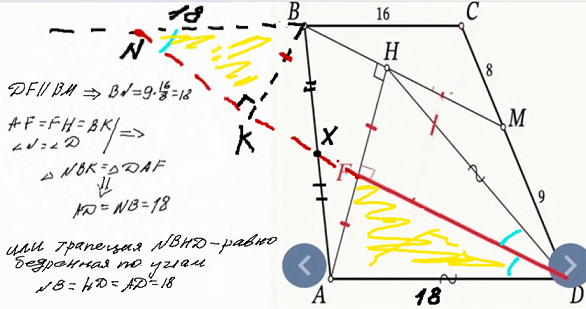
Дополнение. Читатель Сергей С. на канале Наблюдатель порадовал «бесподобным» решением задачи. Так я называю решения, в которых не используется подобие. Идея решения понятна из рисунка.