Обобщение задачи Серёжи Чуйкова
Однажды ученик 6 класса Серёжа Чуйков придумал такую задачу.
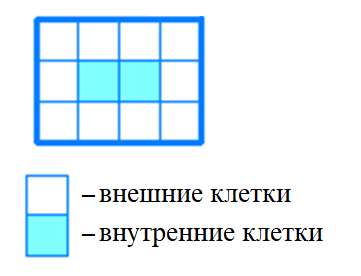
1. Существует ли на клетчатой бумаге прямоугольник, составленный из клеток-квадратов, в котором число его внешних клеток равно числу внутренних клеток?
Рисунок поясняет, какие клетки называют внешними, какие — внутренними. Тогда мы с шестиклассниками решили задачу доступным им методом. В книге «Математика — это интересно!» приведён и другой способ решения задачи, доступный семиклассникам. Привожу его с небольшим изменением.


Рассмотрим прямоугольный параллелепипед N, составленный из внутренних кубиков M.
Три измерения N — натуральные числа a – 2, b – 2 и c – 2. Число кубиков в N равно
n = (a – 2)(b – 2)(c – 2). Число внешних кубиков у M равно m – n = abc – (a – 2)(b – 2)(c – 2).
Теперь задача.



Удастся ли уменьшить число единичных кубиков при других значениях a?
3. Найти наименьшее и наибольшее число единичных кубиков, из которых составлен прямоугольный параллелепипед, у которого количество внешних кубиков равно количеству внутренних кубиков.
Дополнение от 14.01.2021. За время коронавирусных зимних каникул результаты по задачам из этой статьи дополнились. Наименьшее и наибольшее число кубиков в M оказались равны соответственно 960 и 8580.
