Математики тоже шутят?

Лишний раз убеждаюсь, что характер мой испортился окончательно, ремонту не подлежит. Прочитал я заголовок статьи про сумму натуральных чисел, которая равна отрицательной дроби, и, имея остатки юмора, сохранившиеся после 44 лет работы в школе, соображаю, что человек явно шутит.
Но по тексту выходит, что не шутит, а как бы устанавливает факт, да ещё со ссылкой на непререкаемого Леонарда Эйлера. Если учитель математики захочет озадачить школьников, попросит их найти ошибку в рассуждениях, то есть попросит разгадать софизм, следуя авторскому изложению, то я только «за».
Но автор не признаётся нам, что доказывает софизм. Он на полном «серьёзе» приводит нас к «курьёзе» и оставляет в задумчивости. Это похоже на издевательство над читателем. Будем считать, что я один из чувствительных читателей, не любящих таких текстов.
Что доказал автор? Он вычисляет сумму S = 1 + 2 + 3 + 4+ …, используя сумму –3S = 1 – 2 + 3 – 4 + … Привожу цитату в виде картинки.
Дальше следите за руками автора статьи, и вы получите, что S = –1/12.
Мне, как старому ворчуну, почему-то не хочется восхищаться чувством юмора автора, да и названием его блога «Математика не для всех», отдающим высокомерием. Только прошу комментаторов не корить меня за отсутствие чувства юмора и незнание математического фольклора. Я ещё отличаю чувство юмора от стёба ради хайпа, от «юмора», граничащего с издевательством над читателем.
Мне почему-то неудобно за автора перед читателем, который не поймёт, wo der Hund begraben ist (где тут зарыта собака). Попробуем восстановить ход доказательства Леонарда Эйлера. Сумма, стоящая в левой части равенства на картинке, похожа на производную функции

Автор «доказательства» умалчивает условие | x | < 1, при котором получена «формула Эйлера», и применяет её при условии x = 1. Вот и вся разгадка софизма. Получается, как в том анекдоте: ложечки нашлись, а осадок остался.
Дополнение 1. В первом же отклике я получил важную информацию.
Андрей Бахматов: «Цитата из Википедии: «Специальные методы суммирования, использующиеся в некоторых разделах математики, позволяют присвоить конечные значения расходящимся числовым рядам. В частности, один из таких способов предоставляет метод, основанный на регуляризации аналитического продолжения дзета-функции Римана и суммирование по методу Рамануджана, позволяют сопоставить данному ряду некое конечное значение». https://en.wikipedia.org/wiki/Ramanujan_summation
Вы против классификации расходящихся рядов?
Ответ лучше из комментариев перенести сюда и дополнить, иначе диалог потеряется через несколько откликов моих критиков. Не всех же читателей проблема заинтересует так, чтобы дочитать до конца все комментарии.
Мой ответ. Андрей Бахматов, нет конечно, но разве я не прав с «формулой Эйлера»? Хочется понять, как получен результат. А присвоить для каких-то целей можно всё, что угодно, всему, чему угодно. Только вряд ли стоит писать, что сумма ряда 1 + 2 + 3 + … равна числу -1/12. Тогда писать надо что-то другое. Спасибо за урок. Буду знать.
Немного разовью тему. Поскольку я не «чистый математик», а «чистый учитель математики», то имею более конкретный тип мышления, приближенный к «земле», к потребностям обучения детей. Всегда смотрю на проблему с точки зрения «а я могу так объяснить детям?» Мой слегка саркастический материал уже второй посвящён статье с сайта «Математика не для всех». Иногда, как сегодня, я читаю материал и вспоминаю известную реплику чеховской героини: «Они хочут свою образованность показать и всегда говорят о непонятном».
Понимая в математике чуть больше чеховской Дашеньки, я знаю, что иногда данное определение доопределяют, чтобы получить дополнительные возможности применения понятия. Приведу пример.
Определение 1. n-й степенью a числа называют произведение n чисел, каждое из которых равно a.
Понятно, что по этому определению нельзя возвести число в степень 1, поэтому в следующей строке в учебнике пишут:
Определение 2. Считают, что первая степень числа a равна a, и пишут a1 = a.
Без второго определения было бы неправильно делать вид, что равенствоa1 = a понимается в смысле первого определения.
Вот почему я иронизирую над попыткой автора писать на языке «первого определения» равенство тогда, когда он не дал второго определения, не сказал, что он понимает под S в случае расходящегося ряда, не сказал, как надо понимать равенство S = … Если автор критикуемой мною статьи движим желанием рассказать что-то интересное из математики, то честь ему и хвала, только надо ли изумлять публику в стиле героя А.П. Чехова? А если уж очень хочется, то надо быть готовым и к провоцируемой таким «просвещением» народа реплике Дашеньки.
Дополнение 2. Вот и Андрей Бахматов добавил:
Наблюдатель, согласен, писать, что сумма ряда равна -1/12 — это введение в заблуждение. Правильно писать — число, сопоставленное ряду по основанному на регуляризации аналитического продолжения дзета-функции Римана методу равно -1/12.
Ещё раз благодарю Андрея Бахматова за весьма важные уточнения «чистого математика».
Дополнение 3. «Что же из этого следует? — Следует жить…» Какую пользу можно извлечь из состоявшегося разговора? Учитель математики после изучения темы «Производная» может дать сильным учащимся задачу.
Выдающийся швейцарский учёный Леонард Эйлер, долго живший и работавший в России, установил, что при некоторых ограничениях на x верно равенство
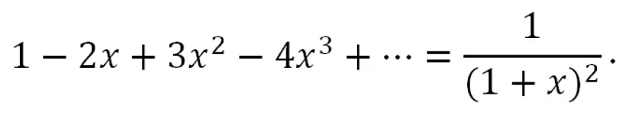
Что это за ограничения и как доказать это равенство?
