Конкурс по решению задач для учащихся 5-6 классов

Как-то раз в Нижнем Тагиле обсуждали мы с учителями, как лучше учить ребят решать задачи из ВПР для пятиклассников.
Разберём решение задачи, которую мы обсуждали тогда, а потом объявим конкурс по решению задач для 5-6 классов.
На двух полках стояли книги — на первой полке в два раза больше, чем на второй. Когда с первой полки на вторую переставили две книги, то книг на полках стало поровну. Сколько книг стояло на каждой полке первоначально?
I способ. Пусть число книг на второй полке составляет одну часть, а на первой полке — две такие же части (рис. слева). 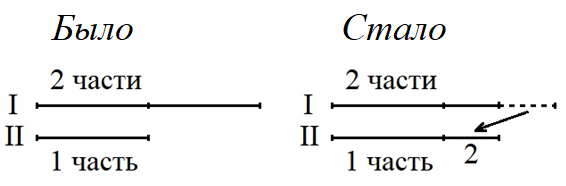
Чтобы уравнять число книг, надо половину одной части переставить на вторую полку (рис. справа), то есть две переставленные книги составляют половину одной части.
1) 2 * 2 = 4 (книги) — приходится на 1 часть (стояло на второй полке первоначально),
2) 4 * 2 = 8 (книг) — стояло на первой полке первоначально.
Ту же задачу решим другим способом.
II способ. Пусть число книг на второй полке составляет одну часть, а на первой полке — две такие же части. Тогда число книг на первой полке составляет 2/3 от числа всех книг. После перестановки двух книг число книг на первой полке составляло уже 1/2 от числа всех книг.
1) 2/3 – 1/2 = 1/6 (всех книг) — приходится на 2 книги.
Всего книг в 6 раз больше.
2) 6 * 2 = 12 (книг) — было на двух полках,
3) 12 : 2 = 6 (книг) — стало на каждой полке,
4) 6 + 2 = 8 (книг) — стояло на первой полке первоначально,
5) 6 – 2 = 4 (книги) — стояло на второй полке первоначально.
Ответ. 8 и 4 книги.
Решите задачи
1. Число учащихся 5а класса составляло 2/3 от числа учащихся 5б класса. Пять учащихся перешли из 5б класса в 5а класс и количества учащихся в этих классах сравнялись. При этом общее число учащихся этих двух классов не изменилось. Сколько учащихся было в каждом классе первоначально?
2. Число книг на первой полке составляло 3/4 числа книг на второй полке. Маша переставила 3 книги со второй полки на первую. Книг на двух полках стало поровну. Сколько книг стояло на каждой полке первоначально?
3. У брата и сестры открыток было поровну. Когда брат подарил сестре 4 открытки, то число его открыток составило 4/5 числа открыток сестры. Сколько открыток было у каждого первоначально?
4. У Алёши и Бори было поровну солдатиков. Когда Алёша подарил Боре 2 солдатика, то число солдатиков Бори составило 6/5 числа солдатиков Алёши. Сколько солдатиков было у каждого первоначально?
5. Число книг на первой полке составляло 3/4 числа книг на второй полке. Маша переставила 3 книги с первой полки на вторую. Теперь число книг на первой полке составляет 2/3 числа книг на второй полке. Сколько книг стояло на каждой полке первоначально?
6. Число книг на первой полке составляло 3/4 числа книг на второй полке. Маша переставила 3 книги со второй полки на первую. Теперь число книг на первой полке составляет 4/5 числа книг на второй полке. Сколько книг стояло на каждой полке первоначально?
7. Если из первого кармана переложить 5 рублей во второй, то сумма в первом кармане составит 2/5 от суммы во втором кармане. Если из второго кармана переложить 5 рублей во первый, то сумма в первом кармане составит 3/4 от суммы во втором кармане. Сколько рублей было в каждом кармане первоначально?
Решения задач (не обязательно всех) можно присылать по адресу avshevkin@mail.ru. Не забудьте указать фамилию, имя решателя, класс, школу, город/село.
Если решения будут — будет что обсудить.
Решению сложных задач поможет чтение статьи:
Задачи про присутствующих и отсутствующих
