ЕГЭ-2021 по математике. Следим за книжными новинками

Эту заметку прислал И.О. Бояринов. Публикуем.
Выпускники-2021 и учителя математики математики получили новый сборник задач ЕГЭ-2021. Это именно СБОРНИК задач, а не пособие по их решению. Обратимся к задаче № 19 из варианта 1.

На с. 209 читаем:
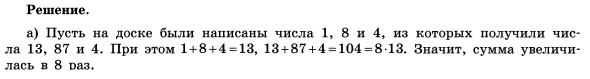
Конечно, это никакое не решение. Это лишь возникшая ниоткуда основа для ответа ДА. Ученику же важно понять, как указанный набор чисел можно найти. Восполним этот пробел. Задачи с вопросительной частицей ЛИ относятся к самым трудным. Здесь попеременно следует искать ситуацию, в которой реализуются указанные условия, и привести соответствующий пример, или доказать, что условие никогда не может быть выполнено. Начнем с примера. С самого простого – когда в каждой группе всего одно число. Пусть это натуральные числа x, y, z.

Исходная сумма равна x + y + z, новая сумма равна 10x + 3 + 10y + 7 + z. Пусть
10x + 3 + 10y + 7 + z = 8(x + y + z).
или
2x + 2y + 10 = 7z.
Очевидно, что натуральное число z должно делиться на 2.
Пусть z = 2. Тогда x + y = 2. По условию x не равен y. Очевидно, что последнее уравнение на множестве натуральных чисел решений не имеет.
Пусть z = 4. Тогда x + y = 9. Последнее уравнение имеет такие решения:
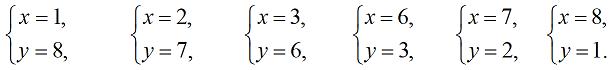
Следовательно, набор чисел (x, y, z), удовлетворяющих условию а) задачи, может быть таким: (1, 8, 4), (2, 7, 4), (3, 6, 4), (6, 3, 4), (7, 2, 4), (8, 1, 4).
Разумеется, для подтверждения ответа ДА достаточно предъявить один из этих наборов. Рассматривать случай z = 6 никакой необходимости нет. Наборов, удовлетворяющих условию а), бесконечно много.
