ЕГЭ по математике. Задача 19. Давайте пошалим…

В ЕГЭ последняя задача под номером 19 — на целые числа. В задаче три вопроса а), б), в), за верные ответы на которые можно набрать до 4 баллов.
Среди задач в сборниках для подготовки к ЕГЭ встречаются и сложные задачи, и простые, но даже в сложных задачах можно получить свои баллы за верное выполнение части заданий. Но сегодня речь пойдёт о другом: о точности понимания формулировок и о точности самих формулировок задач.
Возьмём задачу 19 (вариант 10) из сборника «ЕГЭ-2021» (37 вариантов). Она не новая, была в 26 варианте сборника «ЕГЭ-2017» (50 вариантов). Я включил её решение в свою книжку «Задачи с целыми числами» (Просвещение, 2020) под номером 95. Сегодня прочитал задачу в упомянутом сборнике «ЕГЭ-2021» и задал себе вопрос: а если ученик посчитает, что двузначные числа могут быть и отрицательными (–10, –11,…, – 99), то какие ответы у него могут получиться?
Сначала уточню. С двузначными числами учащиеся знакомы с начальной школы и всегда, по умолчанию, это натуральные числа. Но за годы, проведённые в школе, они познакомились и с отрицательными числами. Что если кто-то из них расширит понятие «двузначные числа», добавив сюда хотя бы одно из чисел –10, –11,…, – 99, что прямо не запрещено условиями задачи? Читаем задачу.
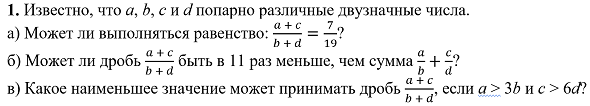
Напомню, я предложил пошалить, представить, что двузначное число может быть отрицательным. Исключительно для разнообразия упражнений и тренировки в подборе чисел, удовлетворяющих условиям задачи. Судя по ответам в сборниках, у составителей задачи двузначные числа положительные. Если попадёт такая задача на контрольной или ЕГЭ, то её надо решать с положительными числами.
А сегодня мы шалим. Чтобы исключить такие шалости на ЕГЭ, я бы внёс уточнение — см. задачу 2. Иначе потом на апелляции объясняй выпускнику, почему число –10 не является двузначным.
Решение.

Теперь попробуйте решить задачу без всяких шалостей.

