ЕГЭ-2022 по математике. Производная. Интеграл

Продолжаем изучать перспективную версию ЕГЭ-2022 от ФИПИ. Ищем по ссылке: Перспективная модель измерительных материалов для государственной итоговой аттестации по программам среднего общего образования по МАТЕМАТИКЕ. Демонстрационный вариант
Matematika_ma-11-ege-pm2022-demo.pdf (userapi.com)
Задание 7 про производную не предвещало неожиданностей. Но с примером 3 обнаружился непорядок. В таблице правильных ответов приведён ответ 7. Посмотрим, как его можно получить. Исправляем опечатку, даже не опечатку, а ошибку набора.
Поскольку дан график производной, то нам нужна информация о знаке производной f ‘(x) на каждом из интервалов. Отметим знаком «+» и «–» знак производной и покажем стрелкой возрастание и убывание функции f (x) на каждом интервале.
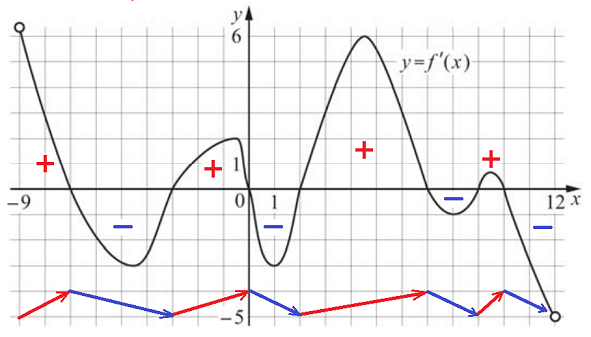
Цветные стрелки на рисунке показывают поведение функции на интервале — возрастание (красная) и убывание (синяя). На отрезке [–8; 11] имеется 4 точки –7, 0, 7 и 10, при переходе через которые возрастание функции сменяется на убывание. На этом отрезке имеется 4 точки максимума –7, 0, 7 и 10. В каждой из них функция достигает наибольшего значения в некоторой окрестности этой точки. Это точки локального максимума. Но вопрос подразумевает наибольшее значение функции — надо бы добавить: наибольшее значение функции на отрезке [–8; 11]. Для этого надо из четырёх значений функции в точках локального максимума выбрать наибольшее (значения функции на концах отрезка здесь меньше, чем в ближайших к ним точках локального максимума). Но вот беда: в условии задачи нет данных для такого способа решения задачи 7.
Дополнение от 23.12.2020. Теперь подумаем, нельзя ли решить задачу с применением интегралов.

Итак, на отрезке [–8; 11] функция f (x) достигает наибольшего значения в точке x = 7. Ответ в таблице верный. И это задача 7 для ЕГЭ? Постановка её в вариант под номером 7 кажется мне большой ошибкой.
Нет, учащихся можно научить в таких задачах быстро получать правильный ответ. Но будет ли указание верного ответа говорить о том, что мы проверили понимание и правильное применение изученной теории? Учтем, что ориентация учащихся, а за ними и учителей на умения, проверяемые при решении задач 1-19 из ЕГЭ, уже убило изучение интегралов. Может быть этой задачей авторы надеются вернуть в учебных процесс качественное изучение интегралов?
Поживём — увидим.
Дополнение от 26.12.2020. После публикации вчерашних новостей про ГВЭ стало понятно, что ЕГЭ уже в 2021 году будет одного уровня, поэтому слов «профильный уровень» в текстах о ЕГЭ 2022 года нет. Что такое ГВЭ поговорим чуть позже.
