Эти коварные проценты!

Рассмотрим несколько задач, включённых мною в книгу «Текстовые задачи» (ИЛЕКСА). Они нам нужны для того, чтобы понять причину конфузов, которые случаются при обращении к процентам.
1. Арбуз массой 20 кгсодержал 99 % воды. Когда он немного усох, то стал содержать
98 % воды. Какова теперь масса арбуза?
На первый взгляд кажется, что масса арбуза мало изменилась, но это только на первый взгляд! Масса «сухого вещества» в арбузе первоначально составляла 100 – 99 = 1 (%), или 20 × 0,01 = 0,2 (кг). После того, как арбуз усох, масса «сухого вещества» составила
100 – 98 = 2 (%) от новой массы арбуза. Тогда новая масса арбуза равна 0,2 : 0,02 = 10 (кг). Арбуз усох вдвое.
2. Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99 % сосны. После рубки сосна будет составлять 98 % всех деревьев». Какую часть леса планирует вырубить леспромхоз?
Если бы экологи лучше знали проценты, то директору леспромхоза не удалось бы их так легко перехитрить. Если будут рубить только сосны, то леспромхоз может вырубить половину леса (см. решение предыдущей задачи). Если же будут рубить и другие деревья, то леспромхоз может оставить в лесу 49 сосен и 1 березу — и в этом случае директор леспромхоза не нарушит своего обещания, так как 49 сосен составляют как раз 98 % от 50 деревьев!
Следующая задача составлена по мотивам выступления 07.07.1997 в программе
«Час-пик» первого вице-премьера правительства России того времени Б.Е. Немцова.
Ведущий программы Андрей Разбаш спросил Бориса Ефимовича:
— Как Вы ожидаете, какой будет через год квартплата, скажем, за двухкомнатную квартиру в Нижнем Новгороде?
Немцов не стал приводить конкретные цифры, он ответил «в процентах»:
— Оплата жилья поднимется за год примерно на 15 %. Сейчас население оплачивает в среднем 35 % реальных расходов на содержание жилья, а через год будет оплачивать уже 50 %.
Итак, задача.
3. В 1997 г. население страны оплачивало в среднем 35 % реальных расходов на содержание жилья, а через год должно было оплачивать уже 50 % этих расходов.
На сколько процентов при этом должна была увеличиться оплата жилья за год?

В чём же заключается «коварство» процентов в этих задачах? Секрет прост: ошибочные решения строятся на сравнении процентов от неравных величин.
В задаче 3 чиновник не ошибся, но считал проценты от стоимости содержания жилья,
а граждане оценивали этот рост, сравнивая в процентах новую квартплату со старой.
У них получалось почти в 3 раза больше!
Теперь приведу примеры «проколов» в печати при обращении к процентам. Вот часть текста из новости на моём сайте. Это отклик на заметку «Математическое лицемерие» Дмитрия Смирнова. https://www.kp.ru/daily/26948.4/3999220/
Дорогая Комсомолка, что с тобой? Ты превратилась в рупор бунтующих «Митрофанушек», которым не нужна еография, так как кучер дорогу знает. Обсуждаемая здесь заметка не единственный пример. Уже скоро месяц как на страницах КП опубликована заметка В. Перекреста — экономического обозревателя, не знающего процентов. На сайте Комсомолки вывешен мой комментарий с указанием ошибки, но она не исправлена даже после моего обращения в газету (с предложением провести урок для журналистов). Вот как это выглядит сегодня (6.03.2019).
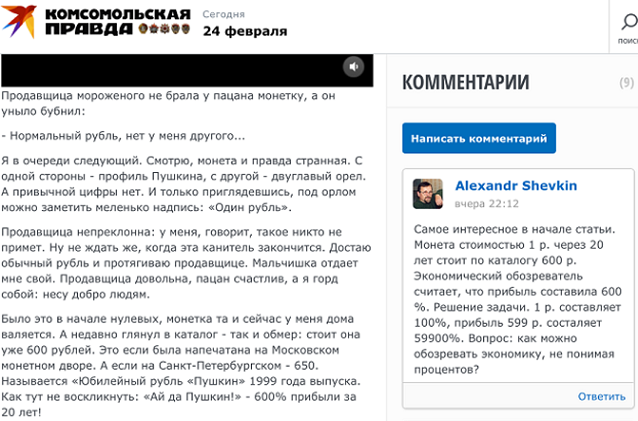
О чём речь? Экономический обозреватель Комсомольской правды написал в газете, что стоимость юбилейного рубля «Пушкин» увеличилась с 1 р. в 1999 г. до 600 р. в 2019 г., то есть на 600 %. «Ай, да Пушкин!», ну и т. п. Но стоимость рубля увеличилась на целых (600 – 1) : 1 * 100 = 59 900 (%)!
В заметке от 11.05.2020 я просил журналистов не искажать статистику смертности населения своими неумелыми вычислениями. Из того, что смертность в Москве в апреле 2019 г. была на 15,5 % меньше, чем в апреле 2020 г. они сделали вывод, что в апреле 2020 г. она была на 15,5 % больше, чем в апреле 2019 г. А это не так.
И вот свежий факт. Привожу цитату из статьи.
Мантуров, который по своей основной профессии социолог, но в правительстве Путина исполняет роль министра промышленности и торговли, вообще обрадовался падению рубля по отношению к доллару на 20 %. Его детская радость было непосредственной, вероятно он хранит свои несметные богатства в американской валюте и внезапно разбогател на 20 %!
Давайте научим Евгения Симакова решению его задачи.
Пусть доллар стоил раньше x руб., а теперь стоит y руб.
(y > x). Что значит, что цена рубля в долларах уменьшилась на 20 %?
Раньше 1 рубль стоил 1/x доллара, а теперь стоит 1/yдоллара, 1/y меньше, чем 1/x на 20 %, значит, 1/y = 0,8/x. Тогда x = 0,8y или y = 1,25x. Цена доллара рублях была x, стала 1,25x — увеличилась на 25 %, но не на 20 %!
Если сейчас доллар стоит 70 руб. (y = 70), то до падения стоимости рубля на 20 % доллар стоил 56 руб. (x = 56). Увеличьте 56 на 25 % (числа 56) — получите 70. Уменьшите число 70 на 20 % (числа 70) — получите 56.
Так что если, по предположению Е. Симакова, Мантуров держит свои деньги в долларах, то указанные изменения стоимости рубля увеличили его «заначку» в рублёвом выражении не на 20, а на 25 процентов.
Как видно из рассмотренных примеров, с помощью процентов можно легко ввести в заблуждение человека, особенно если он плохо в них разбирается. Не случайно в рекламе так часто используют проценты. Одно дело, если обещают повысить пушистость ваших ресниц на 33 %, и совсем другое дело, если обещают, что вы похудеете на 100 %. Изучайте проценты и будьте бдительны!
