Две олимпиадные задачи для пятиклассников

Продолжаем разговор об олимпиадных задачах школьного тура для пятиклассников. Решение первого задания вызвало шквал посещений на сайте.
Олимпиадная задача для пятиклассников… и ещё две задачи
Сегодня привожу условия ещё двух задач. Интересно, что задачу про поросят бурно обсуждают в Интернете, но мнения решателей делятся примерно поровну между двумя ответами.
1. Три поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф соревновались в беге по круговой дорожке. Они стартовали одновременно из одной точки в одном направлении и бежали до тех пор, пока снова не оказались в одной точке (неизвестно, была ли это точка старта или нет). Все три поросёнка бежали с постоянными скоростями, причём Ниф-Ниф бежал быстрее Нуф-Нуфа, но медленнее Наф-Нафа. За время бега Наф-Наф обогнал Нуф-Нуфа ровно 10 раз. Сколько всего было обгонов на этом соревновании?
Вторая задача попроще.
2. В кружки на рисунке требуется вписать числа 1, 2,3,4 или 5 так, чтобы в кружках, соединённых линией, оказались разные числа (иными словами, не должно быть двух кружков, соединённых линией, в которых написаны одинаковые числа). Некоторые кружки уже заполнены. Остальные — пока нет. Заполните их (у себя в тетради или в уме). Какое число будет в кружочке, закрашенном более тёмным цветом? (Обратите внимание, что все кружочки на картинке должны быть заполнены числами (каждый — одним из чисел 1,2, 3, 4, 5). А в поле для ответа нужно вписать только то число, которое должно быть в более тёмном кружочке. Если есть несколько подходящих чисел, впишите в ответ самое большое из них).
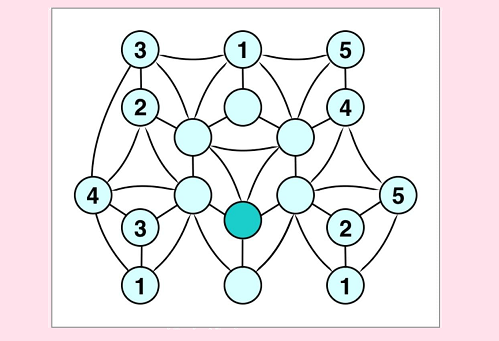
Решения задач
1. Присвоим поросятам номера для краткости записи решения. 1-й — самый медленный, 2-й — побыстрее, 3-й — самый быстрый. Они стартовали в одной точке, двигались по кругу в одном направлении и снова оказались в одной точке. При этом 3-й поросёнок обогнал 1-го 10 раз.
Будем считать, что 10-й обгон состоялся, когда 3-й догнал 1-го в 10-й раз. Тогда если 1-й пробежал n кругов (n не обязательно целое число), то 3-й, сделав, 10 обгонов, пробежал на 10 кругов больше, чем 1-й. Так как 3-й обогнал 1-го в первый раз, когда пробежал столько же, сколько 1-й, и ещё 1 круг. Дальше каждый новый обгон увеличивает разность в пройденной части дистанции на 1 круг. Значит, 3-й обогнал 1-го в 10-й раз, когда пробежал ровно на 10 кругов больше, чем 1-й.
Пусть 2-й в момент, когда 3-й обогнал 1-го, оказался в той же точке и сделал k обгонов 1-го (k — натуральное число). Тогда он пробежал на k кругов больше 1-го. 3-й пробежал больше 2-го на 10 — k кругов, то есть обогнал его 10 — k раз.
Всего обгонов было 10 + k + 10 — k = 20.
Замечание. Мне показалось слишком сложным для пятиклассника считать, что в момент 10- го «догона» ещё не произошло обгона. В условиях задачи лучше бы говорить не о числе обгонов, а о числе кругов, на которое 3-й обогнал 1-го.
2. Сначала поставим числа 5 и 3 в кружки, где невозможно поставить другие числа.
Теперь в кружках над ними невозможно поставить ничего, кроме 4 и 2.
Теперь для тёмного кружка есть одна возможность — число 1.
Для незаполненных кружков есть по 2 варианта — 3 и 5 сверху и 2 и 4 снизу, но в задаче не просили узнать число способов заполнения кружков, а только число в тёмном кругу.
Ответ. 1.
Дополнение. Мне прислали авторское решение задачи. Я решал задачу с предположением «Будем считать, что 10-й обгон состоялся, когда 3-й догнал 1-го в 10-й раз.» Автор задачи считает более точно: трое оказались в одной точке после того, как 3-й обогнал 1-го 10 раз и догнал его на следующем круге.
Привожу авторское решение задачи.
Решение:
Поскольку Наф-Наф (самый быстрый) обогнал Нуф-Нуфа (самого медленного) ровно 10 раз, то он пробежал ровно на 11 кругов больше.
Пусть Ниф-Ниф пробежал на N кругов больше Нуф-Нуфа (и, соответственно, на 11 – N кругов меньше Наф-Нафа). Тогда Ниф-Ниф обогнал Нуф-Нуфа (11 – N) – 1= 10 – N раз, а Наф-Наф обогнал Ниф-Нифа N – 1 раз. Это дополнительно (10 – N) + (N – 1) = 9 обгонов к тем 10.
Итого: 10 + 9 = 19 обгонов.
Ответ: 19 обгонов.
Что поймут здесь пятиклассники, не знаю. Им можно помочь понять без букв, почему 3-й обогнал 2-го на 1 раз меньше, чем 1-го. дело в том, что 3-й сначала обогнал 1-го, а потом после каждого обгона второго обгонял первого, поэтому обгонов 2-го было на 1 меньше, чем обгонов 1-го.
Как можно поправить моё решение. Рассмотрим момент 11-го догона 1-го 3-им (все трое оказались в одной точке. До этого момента 3-й сделал 10 обгонов, а ещё 9 обгонов 2-го (объяснение чуть выше), всего было 19 обгонов. В моём ответе содержится лишний обгон — это последний догон, посчитанный обгоном.
Расхождение в ответах получилось из-за моего дополнительного условия: 10-догон 1-го я посчитал 10-м обгоном. Но это уже немного другая задача.
Итог: хотелось бы на олимпиаде школьников видеть задачи или исключающие неправильное толкование, или дающие указания, исключающие неправильное толкование.
