Две олимпиадные задачи для одиннадцатиклассников
Вчера прошла Всероссийская олимпиада по математике для 11-классников (школьный тур). Мне прислали две симпатичные задачи. Делюсь.
Решения задач
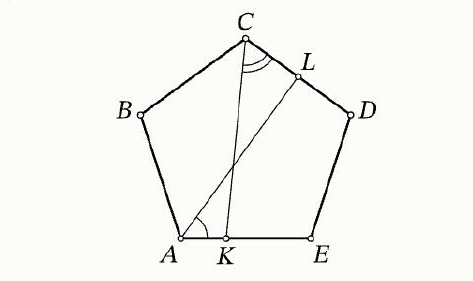
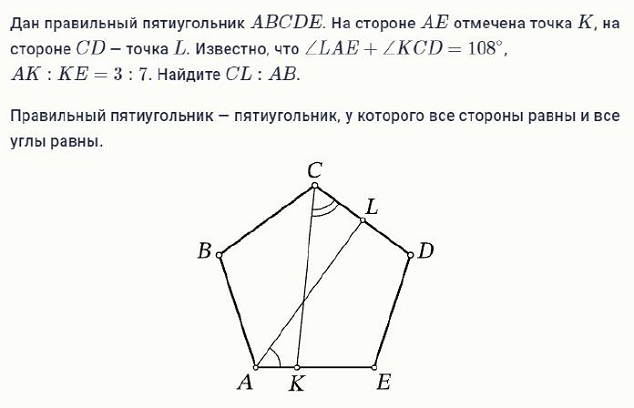
1. Короткое решение заключается в том, что сумма углов 1 и 2, по условию задачи, равна 108 градусам. Углы правильного пятиугольника содержат 108 градусов, следовательно, углы 1 и 4, 2 и 3 попарно равны. Тогда четырёхугольники LDEA и KABC равны. Поэтому LD = KA и LD составляет 0,3AB, тогда CL = 0,7AB. Ответ: 0,7.
Тут есть вопрос: а как обосновать равенство четырёхугольников, для которых в курсах школьной геометрии нет признаков равенства? Это можно сделать так. Рассмотрим поворот на 144 градуса вокруг центра правильного пятиугольника, при котором отрезок DE переходит в отрезок AB, отрезок EA — в отрезок BС. Луч AL, образующий угол 2 со стороной AE, — в луч CK, образующий такой же угол 3 со стороной BС. При этом точка L луча AL, лежащая на стороне CD, перейдёт в точку K луча CK, лежащую на стороне EA, в которую переходит сторона CD.
При повороте четырёхугольник LDEA перешёл в четырёхугольник KABC, следовательно, они равны. Получение ответа описано выше.
Ответ. 0,7.
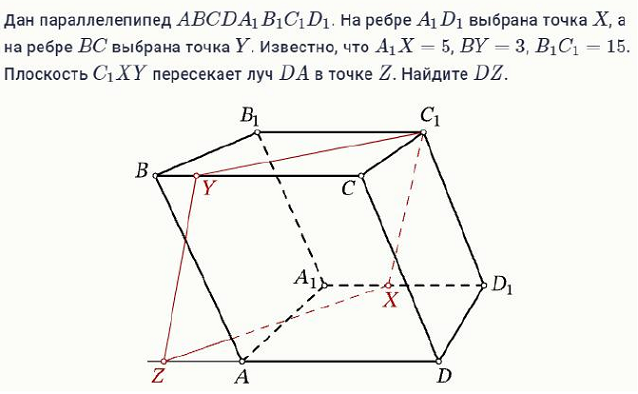
2. Сначала надо заметить, что параллелепипед рисовал художник, у которого точка схода, в которой по правилам перспективы сходятся параллельные прямые AA1, BB1, CC1 и DD1, расположена слишком близко к многограннику, поэтому параллельные прямые не выглядят параллельными. Авторы задачи, видимо, упражняют школьников искусству верных рассуждений на неверном чертеже.
Отметим на рисунке длины данных отрезков и тех отрезков, длины которых можно найти из условия задачи: 5, 10, 3, 12. Проведём отрезок YE, параллельный C1D1. Плоскость YED1 пересекает основания параллелепипеда по параллельным прямым YC1 и ED1. Плоскость YZX пересекает основания параллелепипеда по параллельным прямым YC1 и ZX. Тогда ZX и ED1 параллельны и в параллелограмме XZED1 сторона ZE равна 10. Так как ED = YC = 12, то DZ = 22.
Ответ 22.
