Из домашней работы физматшколы и других источников
Давненько мы не брали в руки шашек…
Решения задач (без трёх геометрических) выложены в разделе Решайте с нами! Решайте, как мы! Решайте лучше нас! Геометрию выложим позже — там в третьей задаче оказалось неполное условие. Ошибка исправлена.
На мою почту avshevkin@mail.ru приходят не только сомнительные предложения поправить моё физическое или финансовое здоровье. Присылают и задачи.
Вчера я получил письмо с задачками, которые дают решать детям в школе, всерьёз занимающейся подготовкой своих учащихся к олимпиадам. Поскольку я не эксперт в олимпиадной тематике, то не могу сказать, насколько новы задачи. Для меня это новые задачи, с ними было интересно повозиться.
Вопрос ребёнка был такой: может ли ответ в задаче про хулиганов зависеть от того, как мы понимаем условия задачи? В задаче можно считать, что каждый хулиган вырывает не менее двух страниц, а можно считать, что Вася может выиграть, вырвав лист 99/100 своим первым ходом. Не уверен, что ребёнок точно переписал от руки условия задач, а я их верно отредактировал. Уточнения и варианты условий приведённых задач можно обсудить. Ну, не буду портить вам удовольствия от решения задач.
1. Хулиганы Петя и Вася по очереди вырывают по одному листу из учебника математики. В учебнике 300 страниц, занумерованных по порядку числами от 1 до 300 (всего 150 листов). Цель Пети, который начинает игру, — получить число 100 в виде суммы нечётных номеров некоторых вырванных им страниц. Цель Васи — получить число 100 в виде суммы чётных номеров некоторых вырванных им страниц. Побеждает тот, кто первым достигает цели. Кто из хулиганов может победить при правильной игре (как бы не играл соперник)?
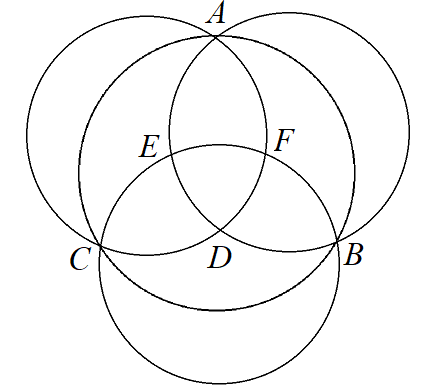
2. Числа от 1 до 10 расставили по одному в каждую из 10 областей, получившихся при пересечении четырёх окружностей (см. рис.). Оказалось, что суммы чисел, записанных внутри трёх пар окружностей, пересекающихся в точках A и D, B и E, C и F, равны. Какими могут быть эти суммы. Приведите примеры.
3. В десяти коробках лежат конфеты, в каждой коробке все конфеты разные, пустых коробок нет и ни в каких двух коробках нет одинакового числа конфет. Докажите, что можно взять из каждой коробки по конфете так, чтобы все взятые конфеты были различными.
4. В ряд выложили 20 белых и 20 чёрных шаров. На каждом из них написали, сколько шаров противоположного цвета находится левее его. Чему равна сумма чисел на всех шарах?
Решения задач можно присылать на почту, адрес которой приведён в начале заметки. Через несколько дней решения задач поместим в разделе
Решайте с нами! Решайте, как мы! Решайте лучше нас!
Дополнение 1. Уже после публикации материала оказалось, что я неверно воспроизвёл по памяти условия задачи с окружностями. Меня поправили. Так появилась ещё одна задача с тем же рисунком.
5. Четыре круга образовали в пересечении десять частей (см. рис.). Внутри частей написали числа от 1 до 10 (по одному в каждой части) так, что сумма чисел в каждом круге одна и та же. а) Какая? б) Приведите пример такой расстановки чисел.
Дополнение 2. Добавляем к хорошим задачам из хорошей школы задачи, присланные хорошим методистом. Их решения рассмотрим отдельно и позже решений предыдущих задач.
1. Дан вписанный четырехугольник ABCD. Лучи АВ и DC пересекаются в точке Р, а лучи ВС и AD – в точке Q. Оказалось, что четырехугольник PBDQ является вписанным. Найдите угол PQA, если угол BAD равен 60о, а угол BAC равен 18о.
2. На плоскости задан произвольный выпуклый четырёхугольник ABCD, пусть MN и KL его средние линии, точка их пересечения Z. Доказать, что DX : XL = 2 : 1, AZ : ZX = 3 : 1.
3. На плоскости задан произвольный выпуклый пятиугольник ABCDE, точки O, M и N — середины сторон AC, CD и DE соответственно, точки K и L — середины отрезков OM и ON, Z — точка пересечения прямых CL и KE, X — точка пересечения прямых OZ и ME. Доказать, что:
1) CZ : ZL = EZ : ZK = 4 : 1, 2) EX : XM = 2 : 1, 3) OZ : ZX = 3 : 2.
