Новости
Четыре задачи на площади
Рассмотрим решения четырёх задач на площади.
1. Докажите, что из медиан любого треугольника можно составить треугольник. Какую часть площади данного треугольника составляет площадь треугольника, составленного из его медиан?
2. Вычислите площадь треугольника, медианы которого равны 9, 12, 15.
3. Вычислите площадь треугольника, высоты которого равны 12, 15, 20.
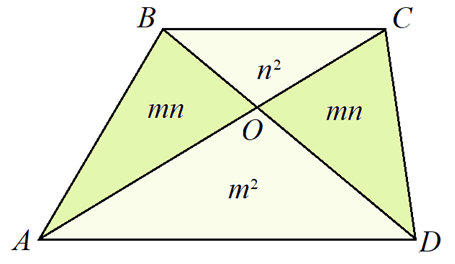
4. Диагонали трапеции пересекаются и делят его на четыре треугольника. Площади треугольников, прилежащих к основаниям трапеции, равны m^2 и n^2 (см. рис.), где
m + n = 10. Вычислите площадь трапеции.
Решения задач приведены здесь: Четыре задачи на площади
