Бесподобные задачи по геометрии
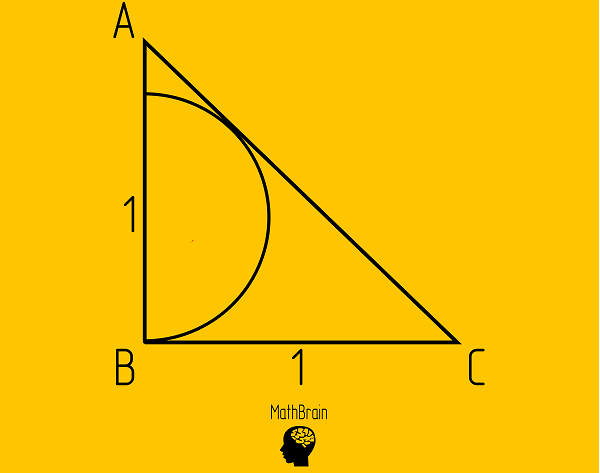
С 9 ноября провисела задача, в которой требовалось найти площадь полуокружности. Только вчера название заметки исправлено.
Найдите площадь полукруга — школьная задача по геометрии | MathBrain | Яндекс Дзен (yandex.ru)
Вот эта задача.
Задача 1. В треугольнике ABC угол B прямой, AB = BC = 1. Полуокружность с центром, лежащем на AB, касается AC. Найдите площадь полукруга.
Под заметкой масса решений задачи, это посмотрите сами, если интересно, какие выкрутасы можно делать на ровном месте. Радиус полуокружности можно найти из подобия треугольников, но более ценным мне кажется применение фактов изученных до подобия. Вот мой комментарий к рисунку, на котором приведён конспект решения.
Бесподобная задача — в смысле решается без подобия треугольников. Надо знать теорему Пифагора для вычисления гипотенузы, свойство касательных, проведённых из одной точки (DC = BC), знать, что острый угол равнобедренного прямоугольного треугольника 45 градусов. А дальше хотите вычислите площадь полукруга, хотите длину полуокружности, а площадь полуокружности пусть считает автор заметки.
Я поместил своё решение, но задача висит так давно, а моё решение находится так далеко, что за два дня его никто и не увидел. Выкладываю его отдельно, чтобы донести до возможно большего круга читателей.
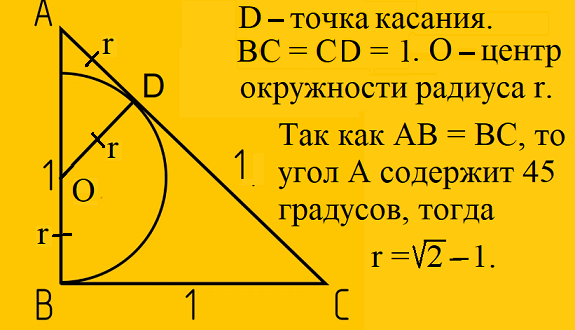
Остаётся половину пи умножить на квадрат радиуса и ответ получен.
Есть и второй короткий способ. Проведём отрезок OC, он разобьёт треугольник ABC на две части. Вычислим площадь треугольника ABC двумя способами и приравняем полученные результаты.
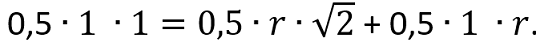
Осталось выразить r и получить ответ.
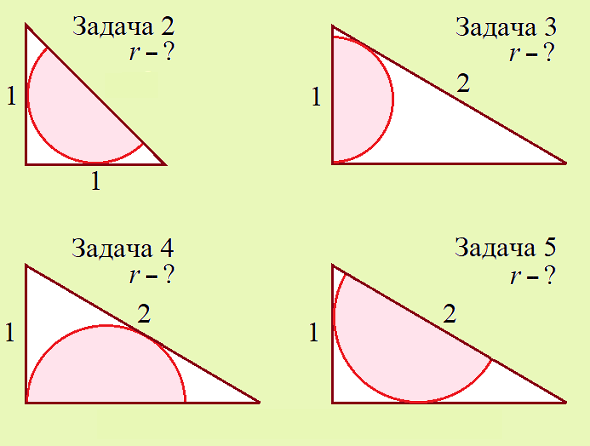
Давайте разовьём тему. Решите для тренировки задачи 2-5.
А вот и задача попроще, в ней все радиусы — рациональные числа.
Задача 6. Найдите радиус окружности, касающейся двух сторон прямоугольного треугольника со сторонами 3, 4, 5, если центр окружности лежит на стороне, длина которой равна: а) 3; б) 4; в) 5.
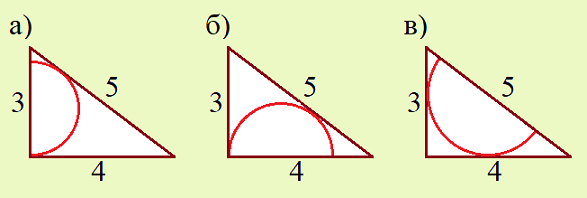
Дополнение. Каждая из задач имеет простое решение через площадь треугольника (четырёхугольника) и радиус вписанной окружности, если построить фигуру, симметричную данной относительно прямой, которой принадлежит центр полуокружности.
