Архимед завещал загадку

Вчера «Российская газета», не имеющая отношения к чисто педагогическим, тем более математическим изданиям, предоставила свои страницы для сообщения о попытке решения знаменитой задачи Архимеда о трисекции угла:
При помощи циркуля и линейки разделить произвольный угол на три равные части.
Бывшая учительница математики Ляля Гиззатовна Зарипова из Миасса показала свой способ построения. Видео и фото здесь:
Вот как построение угла описано в газете.

Внесём уточнения: не на биссектрисе угла, а на её продолжении. Вне окружности получится вершина угла, но его не стоит называть внешним углом, так как это занятый термин (это угол, смежный с внутренним углом треугольника). И последнее: построение не даёт оснований утверждать, что построенный угол в 3 раза меньше данного. Докажем это, используя половину рисунка учительницы. Рассмотрим построение, предложенное в Википедии.
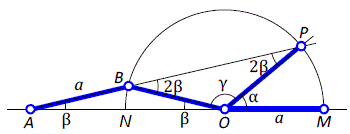
Дан угол MOP, пусть его величина равна α. Строим окружность с центром O, радиусом OM = a (выделяю a полужирным шрифтом, чтобы не путать с альфа: α). На луче MO вне окружности выберем точку A так, чтобы секущая AP пересекала окружность в точке B и AB = a. Способ выбора точки A не обсуждаем, так как нам достаточно показать, что при таком выборе точки A величина угла PAM составит 1/3 величины угла POM.
Итак, пусть ∠PAM = β, в равнобедренном треугольнике ABO ∠BOA = β, тогда ∠OBP = 2β (внешний угол этого треугольника). В равнобедренном треугольнике BOP ∠BPO = 2β. Тогда α = 180° – β – (180° – 4β) = 3β.
Остаётся заметить, что отрезок AN меньше проекции отрезка AB на прямую AM, а эта проекция меньше AB. То есть, если α = 3β, то AN < a.
К великому сожалению, Ляля Гиззатовна ошиблась в своих рассуждениях, так как не привела доказательства равенства α = 3β, опираясь на своё построение. Его и невозможно привести, так как при её построении после двух применений теоремы синусов можно показать, что если соотношение α = 3β выполнено, то равенство AN = a выполняется лишь для таких острых углов величины β, для которых верно равенство cos 0,5β = cos 1,5β, что невозможно.
Однако я благодарен Ляле Гиззатовне и «Российской газете» за хороший повод вспомнить замечательную задачу древности на затянувшихся коронаканикулах.
