Динары
17.02.2005 к нам поступило письмо из г. Кызыла с просьбой помочь решить задачу.
Задача. Один говорит другому: «Дай мне 7 динариев, и я буду в 5 раз богаче тебя». А другой говорит: «Дай мне 5 динариев, и я буду в 7 раз богаче тебя». Сколько денег у каждого?
Начнем с алгебраического решения.
Пусть у первого х динаров, у второго у динаров. После передачи семи динаров у них станет соответственно (х + 7) динаров и (у – 7) динаров, тогда верно равенство
х + 7 = 5(у – 7).
А после передачи 5 динаров у них станет соответственно (х – 5) динаров и (у + 5) динаров, тогда будет верно равенство
7(х – 5) = у + 5.
Решив систему из двух полученных уравнений, получим х = 7 2/17, у = 9 14/17.
Числовые данные здесь не очень хороши, но если это старинная задача, то, как говорится, из песни слова не выбросишь.
Рассмотрим красивое арифметическое решение этой задачи. Изобразим общую сумму денег двух людей в виде отрезка. Тогда после передачи семи динаров у первого станет в пять раз больше, чем у второго — у первого 5 частей, у второго 1 часть, то есть у второго останется одна часть из шести, 1/6 общей суммы.
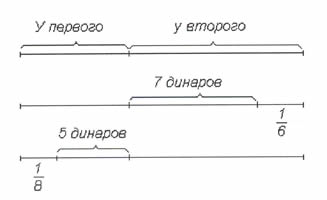
После передачи пяти динаров у второго станет в 7 раз больше, чем у первого, то есть у первого останется 1/8 общей суммы.
Тогда 5 + 7 = 12 динаров составляют 1 – 1/6 – 1/8 = 17/24 общей суммы, то есть всего у них было 12 : 17/24 = 288/17 = 16 16/17 динара, поэтому у первого была 1/8 этой суммы, да еще 5 динаров, то есть 7 2/17 динара, а у второго 16 16/17 – 7 2/17 = 9 14/17 динара.
Ответ. 7 2/17 и 9 14/17 динара.
