Короткое решение задачи С4 из книги Т.А. Корешковой и др.
В книге «ЕГЭ 2009. Математика. Типовые тестовые задания»[1] приведены 10 вариантов ЕГЭ, с помощью которых выпускники могут готовиться к ЕГЭ. Обратим внимание на задачу С4 из I варианта.
С4.* В правильной четырехугольной призме АВСDА1В1С1D1 сторона АВ основания равна б, а боковое ребро АА1 равно 12. Через вершины А и С1 призмы проведена плоскость, пересекающая боковое ребро ВВ1 в точке К, а боковое ребро DD1 в точке L. Найдите объем пирамиды А1АКС1L.
В книге приведено следующее решение этой задачи.

Приведем теперь более простое и короткое решение.
Решение. Так как плоскость сечения пересекает противоположные боковые грани призмы по параллельным прямым, то четырехугольник AKC1L – параллелограмм. Тогда площади равных треугольников AKL и C1LK равны, а объемы пирамид с общей вершиной A1 и равновеликими основаниями AKL и C1LK, лежащими в одной плоскости, равны. Это означает, что объем пирамиды KAA1L составляет половину искомого объема.
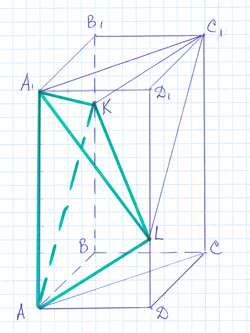
Объем пирамиды KAA1L не зависит от положения точки K на отрезке AA1 (высота треугольника AA1L, проведенная из L к основанию треугольника, равна AD, а высота пирамиды KAA1L, проведенная из K к плоскости основания пирамиды AA1L, равна A1B1). Поэтому этот объем пирамиды KAA1L равен объему пирамиды A1ABD и равен
1/3×1/2×AB AD×AA1 = 1/6×6×6×12 = 72.
Тогда объем пирамиды А1АКС1L равен 72×2 = 144.
[1] ЕГЭ 2009. Математика. Типовые тестовые задания. / Т.А. Корешкова, Ю.А. Глазков, В.В. Мирошин, Ю.В. Шевелева. – М.: Издательство «Экзамен», 2009, – 78.
