Задачи С6 из контрольной работы 24.04.2010 и решения Эвнина и Саржевского


Решение Саржевского Владимира Ивановича.

А.В. Шевкин. Задания С6 из ЕГЭ 2010 по математике
Решайте с нами, решайте как мы, решайте лучше нас!
Шевкин А.В.
Идея написать эту статью возникла у меня на осенних школьных каникулах 2009 года, удлинившихся из-за эпидемии гриппа. Отложив срочные дела на некоторое время, взял я два сборника тренировочных заданий и засел за решение олимпиадных задач С6. Первоначально хотелось вывесить «для затравки» решения нескольких задач на сайте «Математика. Школа. Будущее» (www.shevkin.ru ) и пригласить посетителей сайта принять участие в решении остальных задач. Поскольку задачи рассматриваемой тематики я сам решал впервые, то не было уверенности в том, что предложенные мною решения окажутся простыми и понятными, что я решу все задачи. Как только получились решения первых 5-6 задач, условия всех 20-ти задач — первые 10 вариантов из сборника 1), следующие 10 из сборника 2) — были разосланы знакомым учителям и методистам с предложением подключится к работе.
Первые отклики были получены от автора учебников Г.К. Муравина и В.И. Романовского (Израиль, г. Реховот, преподаватель математики, один из авторов сайта www.math-on-line.com, автор книги «Арифметика помогает алгебре», М.: Физматлит, 2007). Причем с В.И. Романовским завязалась оживленная переписка, приведшая к тому, что общими усилиями число решенных задач было доведено до 17.
Через несколько дней после публикации 21.11.2009 статьи на сайте А.Г. Рубин прислал решение задачи из варианта 16, которое с его согласия включено в статью. А 29 ноября 2009 г. учитель математики МОУ «Гимназия г. Троицка» Ю.О. Пукас прислал ответ на полемическую статью «Не корысти ради — за державу обидно!», опубликованную на сайте. В ней содержалась идея более простого решения задачи из варианта 14 и решение последней нерешённой пока задачи (вариант 6). В марте 2010 г. Ю.К. Майоров (Москва, лицей 1523) прислал замечание по комментарию к варианту 10, которое мы учли, и свои решения задач из трёх вариантов. Последнее (по времени) исправление решения (в варианте 13) сделано 4 декабря 2010 г. после письма Г.Г. Шеремет, обнаружившей ошибку в первоначальном варианте решения, размещенного на сайте.
В решении задачи из варианта 9 использована статья В.Ю. Кузнецовой «Олимпиадные задачи с факториалами в тренировочных вариантах ЕГЭ» (Архимед. Научно-методический сборник. Выпуск 6. М.: АНО Институт логики, 2010).
Если у читателя этих строк появится желание упростить или исправить опубликованные решения, то пишите по адресу avshevkin@mail.ru.
Интересные решения будут вставлены в текст этой статьи на сайте с указанием фамилии приславшего решение. При этом верные первоначальные решения мы сохраним, так как они тоже содержат поучительные идеи.
1) Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: ЕГЭ: Математика / авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель, 2010. – 93, [3] с. – (Федеральный институт педагогических измерений).
2) ЕГЭ 2010. Математика. Типовые тестовые задания / И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Экзамен», 2010. — 55, [1] с. (Серия «ЕГЭ 2010. Типовые тестовые задания»).



Опечатка. В 5-й строке ниже вместо p > 8 должно быть p > 1.



Комментарии. Поясним, откуда берутся формулы для подсчета числа делителей в случаях а), б) и в).
а) Если некоторое число имеет один простой делитель m кратности k, то оно делится на каждое из чисел 1, m1, m2, … , m k, т. е. это число имеет k + 1 делителей.
б) Если некоторое число имеет t простых делителей первой кратности m1, m2, …, mt, то оно делится на
1, m1, m2, …, mt,
m1m2, m1m3, …, m1mt,
m1m2m3, …, m1m2, …,
m1m2m3…mt.
в) Если простые делители m и n некоторого числа имеют кратности a и b, то это число делится на каждое из чисел, записанных в следующих двух строках
1, m1, m2, … , m a,
1, n1, n 2, … , n b,
а также на все возможные произведения чисел, взятых по одному из каждой строки. Так как в первой строке a + 1 число, а во второй — b + 1 число, то всего делителей p = (a + 1)(b + 1).

Комментарии. Поясним, откуда берутся формулы для подсчета числа делителей в случаях а), б) и в).
а) Если некоторое число имеет один простой делитель m кратности k, то оно делится на каждое из чисел 1, m1, m2, … , m k, т. е. это число имеет k + 1 делителей.
б) Если некоторое число имеет t простых делителей первой кратности m1, m2, …, mt, то оно делится на
1, m1, m2, …, mt,
m1m2, m1m3, …, m1mt,
m1m2m3, …, m1m2, …,
m1m2m3…mt.
в) Если простые делители m и n некоторого числа имеют кратности a и b, то это число делится на каждое из чисел, записанных в следующих двух строках
1, m1, m2, … , m a,
1, n1, n 2, … , n b,
а также на все возможные произведения чисел, взятых по одному из каждой строки. Так как в первой строке a + 1 число, а во второй — b + 1 число, то всего делителей p = (a + 1)(b + 1).
Вариант 11
С6. Найдутся ли хотя бы три десятизначных числа, делящиеся на 11, в записи каждого из которых использованы все цифры от 0 до 9?
Решение. Число делится на 11 тогда и только тогда, когда разность между суммами его цифр, стоящих на нечётных и на чётных местах, делится на 11.
Запишем все цифры подряд: 9876543210. В написанном числе указанная разность сумм равна 5. Меняя местами, например, 5 и 8, мы одну сумму увеличиваем на 3, а другую уменьшаем на 3. Значит, разность между суммами его цифр, стоящих на нечётных и на чётных местах, становится равной 11. Меняя местами, например, 4 и 1, или 3 и 6, получаем требуемые примеры.
Примечание. В задаче не требуется нахождение всех чисел, обладающих указанным свойством.
Ответ. Да.
Комментарии. 1. Мы привели авторское решение из сборника 2). Ещё раз выразим удовольствие, если решения в таком «телеграфном стиле» будут засчитываться и на экзамене. Но задачи такого типа на экзамене могут создать конфликт, так как если выпускник случайно наткнётся на число (возможно, неведомым ему самому способом), например, на число 1968573420 и двумя перестановками пар цифр получит ещё два числа: 6918573420, 6958173420, то задача будет решена. Ведь задача с вопросом «существует ли?» считается решенной, если предъявлен объект, существование которого доказывается. Предъявление числа и доказательство наличия требуемых свойств и есть доказательство. Как в этом случае эксперты будут оценивать решение задачи?
2. В сборнике 2) была опечатка: вместо «4 и 1» было «4 и 7».
Вариант 12
С6. Найдите все натуральные числа, которые делятся на 42 и имеют ровно 42 различных натуральных делителя (включая единицу и само число).
Решение. (Романовский В.И.) Искомые числа делятся на 42 и имеют, по крайней мере, простые делители 2, 3 и 7. Обозначив кратности этих делителей (без привязки к ним) m, n и k, найдём эти кратности из уравнения для количества делителей числа:
N = (m + 1)(n + 1)(k + 1) = 42 = 2×3×7.
Принимаем m = 1, n = 2, k = 6 (вариант единственный с точностью до привязки к буквам). Искомые числа (их количество равно числу перестановок из трёх элементов P3 = 3! = 6) равны: 2×32×76; 2×36×72; 22×3×76; 22×36×7; 26×3×72; 26×32×7.
Ответ. 2×32×76; 2×36×72; 22×3×76; 22×36×7; 26×3×72; 26×32×7.
Вариант 13
C6. Решите уравнение 3m + 4n = 5k в натуральных числах.
Решение. Левая часть уравнения при любых натуральных m и n при делении на 3 даёт остаток 1, следовательно, такой же остаток при делении на 3 должен быть и у 5k, откуда следует, что k — чётное. Пусть k = 2r, r — натуральное число.
Правая часть уравнения при любом натуральном k при делении на 4 даёт остаток 1, следовательно, такой же остаток при делении на 4 должен быть и у 3m, откуда следует, что m — чётное. Пусть m = 2s, s — натуральное число.
Перепишем исходное уравнение в виде 32s + 4n = 52r, или в виде 22n = (5r – 3s)(5r + 3s). Тогда
5r – 3s = 2q и 5r + 3s = 2l, где q и l — целые неотрицательные числа и q + l = 2n. Таким образом,
5r = (2q + 2l):2, 3s = (2l – 2q):2 = 2l – 1 – 2q – 1.
Число 3s — нечётное, значит, 2l – 1 – 2q – 1 нечётно, поэтому q = 1 и 3s = 2l – 1 – 1. Следовательно, число l – 1 чётно, l – 1 = 2p (иначе левая часть не делится на 3). Тогда 3s =
= (2p – 1)(2p + 1) — произведение двух множителей, отличающихся на 2 и являющихся степенями тройки. Ясно, что эти множители 1 и 3, тогда p = 1, s = 1, m = 2s = 2. Далее последовательно получаем: l = 2p + 1 = 3, 5r = (2q + 2l):2 = 5, r = 1, k = 2r =2, q + l = 2n = 4. Итак, m = n = k = 2.
Ответ. m = 2, n = 2, k = 2.
Примечание. В журнале «Квант» (4/1998) эта задача сформулирована для уравнения
3x + 4y = 5z (А.Ю. Эвнин, В.А. Сендеров, ММО, 1998, 11 класс.). Приведём решение из журнала.
Правая часть уравнения при делении на 3 должна давать тот же остаток, что и левая, т. е. 1. Поэтому z — чётное. Аналогично, левая часть уравнения делится на 4 с остатком 1, поэтому число x тоже чётное. Обозначив z = 2t, имеем 5t – 2y = 3u, 5t + 2y = 3v. Поэтому u = 0, v = x = 2k. Значит,
1 + 2y + 1 = 32k, откуда (3k – 1)(3k + 1) = 2y + 1. Получили 3k + 1 = 2m, 32k – 1 = 2n,
2m – 2n = 2. Откуда n = 1, k = 1, y = 2, x = 2k = 2, z = 2.





Поэтому каждый прыжок на 4 единицы происходит всегда через точку вида 4n. Так как точки 1 и 2 находятся на одном интервале между соседними точками вида 4n, то, начав движение из точки 1 и завершив его в точке 2 из одного интервала, мы выполним одинаковое число прыжков на 4 единицы вправо и влево, следовательно, общее число прыжков на 4 единицы чётное. Тогда на прыжки на 1 единицу остается четное число прыжков, так как общее число прыжков 2010 чётное.
Выполняя один прыжок на 1 единицу от числа k вправо (влево), мы увеличиваем (уменьшаем) число k на 1. Выполняя один прыжок на 4 единицы от числа k вправо (влево), мы увеличиваем (уменьшаем) число k на 4. Если всего выполнено а прыжков на 4 единицы вправо, а прыжков на 4 единицы влево,
b прыжков на 1 единицу вправо и c прыжков на 1 единицу влево, то выполняется равенство 1 + 4а – 4а +
+ b – c = 2 (последовательность выполнения прыжков, очевидно, не влияет на результат), т. е. верно равенство b = c + 1. Но тогда общее количество прыжков на 1 единицу равно b + c = 2c + 1 — число нечётное, а выше установлено, что это число чётное. Следовательно, выполнить требуемое невозможно.
Ответ. Нет.
Вариант 19
С6. Найдите все натуральные числа, последняя десятичная цифра которых 0 и которые имеют ровно 15 различных натуральных делителей (включая единицу и само число).
Решение. (Романовский В.И.) Здесь невозможно ограничиться одним простым делителем кратности k = 15 — 1 (см. вар. 10), поскольку по условию должны быть, по меньшей мере, два простых делителя — 2 и 5. Если ограничиться выбором только этих двух делителей, их кратности в искомых числах дает формула p = (m + 1)(n + 1), где p — количество делителей числа, равное 15, m и n — кратности простых делителей. (m + 1)(n + 1) = 15; m = 2, n = 4 (единственное решение без привязки к конкретным множителям). Существуют два числа, удовлетворяющие условию: N1 = 22×54 = 2500;
N2 = 24×52 = 400.
Ответ. 2500 и 400.
Вариант 20
С6. При каком наибольшем п найдется п семизначных чисел, являющихся последовательными членами одной геометрической прогрессии?
Решение. (Романовский В.И.) Очевидно, решая задачу, следует выполнять требование: первое член прогрессии и её знаменатель должны быть по возможности, минимальны. При этом все члены прогрессии — целые числа. Логичный, на первый взгляд, выбор числа 106 в качестве первого члена и знаменателя прогрессии 1,1 не приводит к успеху. Цепочка чисел заканчивается на 6-м ходу. Верный подход состоит в том, чтобы в качестве первого члена выбрать максимально возможную степень (естественно, основание степени должно быть минимально), а в качестве знаменателя прогрессии — неправильную дробь, знаменатель которой равен основанию степени первого члена, либо ближайшей степенью его, а числитель – знаменателю плюс 1. Выбираем в качестве первого члена прогрессии число 1048576 = 220, а в качестве знаменателя прогрессии число 5/4. Получаем такую цепочку: 1048576, 1310720, 1638400, 2048000, 2560000, 3200000, 4000000, 5000000, 6250000, 7812500, 9765625 — всего 11 членов.
Ответ. 11.
Ю.О. Пукас. Решение задачи С18 из диагностической работы (12.2008) МИОО
Пукас Ю. О., гимназия г. Троицка
С18. При каких натуральных n существует рациональное число x, удовлетворяющее равенству
n2 + 2 = (2n – 1)x? (1)
Решение. 1. Из того, что при всех n: (n2 + 2) > (2n – 1), следует, что искомое число x = k/m больше единицы: k > m.
- Для чисел, удовлетворяющих условию задачи, равенство (n2 + 2)m = (2n – 1)kопределяет натуральное число, единственным образом разлагаемое на простые множители. Это значит, что в разложении на простые множители числа (2n – 1) присутствуют все простые множители числа (n2 + 2), но в меньших степенях. Это значит, что (n2 + 2) делится на (2n – 1).
- Следовательно, n2 + 2 = d(2n – 1), где d — натуральное число. Рассмотрим квадратное уравнение относительно n:
n2 – 2dn + (d + 2) = 0. (2)
Его дискриминант, деленный на 4, должен быть квадратом натурального числа, которое обозначим j. То есть j2 = d2 – d – 2 = (d – 2)(d + 1). Так как j = 0 лишь при d = 2 (d — натуральное число), то уравнение (2) имеет единственный корень n = 2, для которого исходное уравнение (1) не имеет рационального корня.
Тогда (d – j)(d + j) = d + 2. Но j = 1 не дает нам натурального d и, следовательно, натурального n. При j = 2 имеем d = 3, откуда находим, что n = 5, x = 3/2 (при n = 1 исходное уравнение не имеет корней).
Если j > 2, то левая часть равенства (d – j)(d + j) = d + 2 больше правой, так как
d + j > d + 2, и не забудем, что d – j должно быть натуральным числом. То есть для
j > 2 равенство (d – j)(d + j) = d + 2 невозможно.
Итак, лишь при n = 5 исходное уравнение имеет рациональный корень.
Ответ. При n = 5.

Единый государственный экзамен по математике (Демонстрационный вариант МИИО)
Единый государственный экзамен по математике
Демонстрационный вариант 2009 г.
Демонстрационный вариант ЕГЭ по математике 2009 года, разработан по заданию Федеральной службы по надзору в сфере образования и науки Российской Федерации. Ряд заданий требует не только знания школьной программы по математике, но и умения применять математические знания. Некоторые из заданий можно выполнить, не используя материала старшей школы.
Состав экзаменационных материалов
В экзаменационные материалы входят задания 1 – 9, результатом выполнения которых является краткий ответ к задаче, и задания 10 – 17, результатом выполнения которых является полное решение задачи.
Время выполнения работы
На выполнение работы дается 240 мин.
Условие успешного прохождения школьной аттестации
Уровень успешной школьной аттестации соответствует 4-5 правильно выполненным заданиям (точное число будет объявлено перед экзаменом). Аттестационная оценка по 5-бальной шкале не выставляется.
Учет результата ЕГЭ по математике при приеме в вузы
В экзаменационных материалах выделена выпускная («школьная») часть – первые одиннадцать заданий и вступительная («вузовская») часть – последние шесть заданий.
Правильное выполнение заданий оценивается в баллах в соответствии с таблицей:
|
Номера заданий |
Максимальное число баллов за одно задание |
|
1 – 9 |
1 |
|
10 – 12 |
2 |
|
13, 14 |
3 |
|
15, 16 |
4 |
|
17 |
5 |
Частичное выполнение задания может дать меньшее (целое) число баллов, в том числе – ноль.
Оценка работы получается суммированием баллов по отдельным заданиям, с ограничением в сумме 10 баллов для заданий выпускной части. (Таким образом, максимальное число баллов за работу равно 31)
Оценка результата Единого государственного экзамена по математике для выпускника устанавливается как процент выпускников, выполнивших работу не хуже данного выпускника. (Более детальное описание правил оценивания будет опубликовано на сайте Рособрнадзора в ноябре 2008 г.)
Федеральная служба по надзору в сфере образования и науки установит перед началом экзаменов значение оценки результата ЕГЭ по математике, выше которой должен набрать выпускник, чтобы вузы имели право рассматривать его заявление о приеме. Более высокие значения оценки вузы должны учитывать при проведении конкурса среди подавших заявление о приеме в данный вуз.
Замечание и предложения по настоящей демонстрационной версии просим присылать по адресу ege2009@mioo.ru
По просьбам учителей, публикация решений и ответов к настоящей демоверсии отложена до 26 октября.
Желаем успеха!



Короткое решение задачи С4 из книги Т.А. Корешковой и др.
В книге «ЕГЭ 2009. Математика. Типовые тестовые задания»[1] приведены 10 вариантов ЕГЭ, с помощью которых выпускники могут готовиться к ЕГЭ. Обратим внимание на задачу С4 из I варианта.
С4.* В правильной четырехугольной призме АВСDА1В1С1D1 сторона АВ основания равна б, а боковое ребро АА1 равно 12. Через вершины А и С1 призмы проведена плоскость, пересекающая боковое ребро ВВ1 в точке К, а боковое ребро DD1 в точке L. Найдите объем пирамиды А1АКС1L.
В книге приведено следующее решение этой задачи.

Приведем теперь более простое и короткое решение.
Решение. Так как плоскость сечения пересекает противоположные боковые грани призмы по параллельным прямым, то четырехугольник AKC1L – параллелограмм. Тогда площади равных треугольников AKL и C1LK равны, а объемы пирамид с общей вершиной A1 и равновеликими основаниями AKL и C1LK, лежащими в одной плоскости, равны. Это означает, что объем пирамиды KAA1L составляет половину искомого объема.
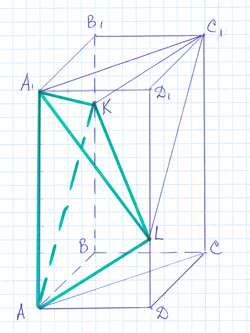
Объем пирамиды KAA1L не зависит от положения точки K на отрезке AA1 (высота треугольника AA1L, проведенная из L к основанию треугольника, равна AD, а высота пирамиды KAA1L, проведенная из K к плоскости основания пирамиды AA1L, равна A1B1). Поэтому этот объем пирамиды KAA1L равен объему пирамиды A1ABD и равен
1/3×1/2×AB AD×AA1 = 1/6×6×6×12 = 72.
Тогда объем пирамиды А1АКС1L равен 72×2 = 144.
[1] ЕГЭ 2009. Математика. Типовые тестовые задания. / Т.А. Корешкова, Ю.А. Глазков, В.В. Мирошин, Ю.В. Шевелева. – М.: Издательство «Экзамен», 2009, – 78.






