Вокруг задачи из учебника геометрии
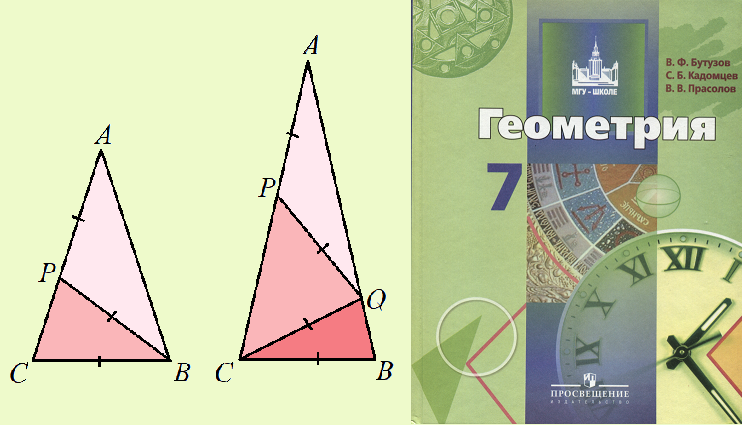
В учебнике «Геометрия, 7 класс (В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолов; Просвещение) под номером 94 помещена задача, которая есть и в учебнике Л.С. Атанасяна и др.
Эту задачу решают в Интернете не всегда коротким способом. Давайте построим вокруг неё цепочку задач, по которой учащиеся могут продвигаться самостоятельно — от простого к сложному. Начнём не с задачи 94, а с более простых задач.
Далее приведены только условия задач.
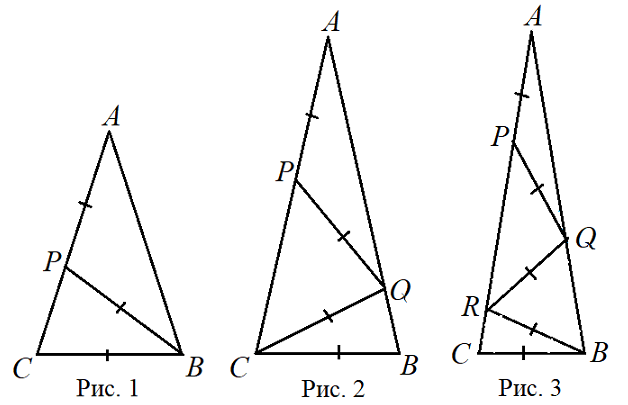
1. На стороне AC равнобедренного треугольника ABC (AB = AC) отметили точку P. Оказалось, что
AP = PB = BC (рис. 1). Найдите угол A и докажите, что BP — биссектриса угла ABC.
2. На сторонах AC и AB равнобедренного треугольника ABC (AB = AC) отметили точки P и Q соответственно. Оказалось, что AP = PQ = QC = CB (рис. 2). Найдите угол A.
3 (94). На рисунке 3 AB = AC и AP = PQ = QR = RB = BC. Найдите угол A и докажите, что BQ = BR.
4. Равнобедренный треугольник ABC разбили на n равнобедренных треугольников, боковые стороны которых равны основанию BC треугольника ABC, а все вершины этих треугольников лежат на сторонах AB и BC треугольника ABC (как в задачах 1-3). Найдите наименьшую градусную меру угла A, выражаемую натуральным числом.
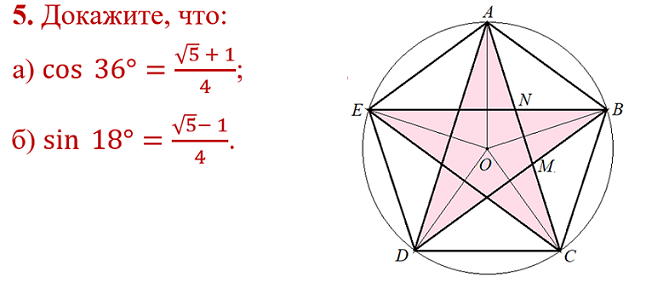
Для читателей старше 7 класса заметим, что равнобедренный треугольник ABC, разбитый на два равнобедренных треугольника, из задачи 1 встречается на рисунке правильного пятиугольника, в котором проведены все диагонали. На странице Задачи на правильные многоугольники есть ссылка на статью с тем же названием. Вот рисунок из этой статьи, на котором находим равнобедренный треугольник ACD, разбитый на два равнобедренных треугольника. Нижний подобен треугольнику ACD. Там же есть задача, которую можно решить при помощи этого треугольника.
И последнее наблюдение. Все равнобедренные треугольники АВС, в которых рассмотренные разбиения возможны, можно найти в правильных многоугольниках с нечётным числом сторон, если провести две наибольшие диагонали из одной вершины многоугольника. Если ещё из вершины угла при основании треугольника АВС провести наименьшую диагональ правильного многоугольника, пересекающую этот треугольник, то от него отсечётся ему подобный треугольник — последний треугольник из рассмотренного разбиения.
Ссылка на статью в разделе «Решайте с нами…» сайта www.shevkin.ru
Вокруг задачи из учебника геометрии
Теги: головоломка, задача по геометрии, математика, ОГЭ
