Старинные задачи и арифметические способы их решения

В данной заметке речь идёт о старинных задачах и арифметических способах их решения.
Такие задачи давали учащимся в те времена, когда ещё не использовали уравнений и их систем, поэтому отдельный интерес представляет арифметические способы их решения. Применение уравнений и их систем — вопрос более понятный.
Начнём с задачи Евклида (III в. до н. э.). Далее приведены задачи из разделов «Задания для повторения» учебников «Математика, 5», «Математика, 6», «Алгебра, 9» (С. М. Никольский и др., Просвещение, 2019).
1. (6 кл., 1274) Ослица и мул шли вместе, нагруженные мешками равного веса. Ослица жаловалась на тяжесть ноши. «Чего ты жалуешься, — сказал мул, — если ты мне дашь один твой мешок, моя ноша станет вдвое больше твоей, а если я дам тебе один мешок, наши грузы только сравняются». Сколько мешков было у каждого?
Поиск в Интернете по запросу «задача Евклида про мула и ослицу» приводит к решениям задачи с помощью линейного уравнения или системы линейных уравнений. Например:
http://www.covereducation.ru/areds-508-7.html
Поскольку эту задачу мы включили в учебник для 6 класса, в котором уравнения (без термина «линейные») изучаются, а системы — нет, то возможно непростое решение при помощи линейного уравнения.
В наших учебниках для 5-6 классов много внимания уделено применению арифметических способов решения задач, поэтому совсем не удивительно, что некоторым учащимся удаётся придумать свой способ решения, порой неожиданный для учителя. Рассмотрим решение К. Марченко (6 класс, муниципальная гимназия, г. Ревякин, Московская обл.). Его мне прислала учительница математики Т.В. Абросимова около 20 лет тому назад, когда учебники назывались «Арифметика».
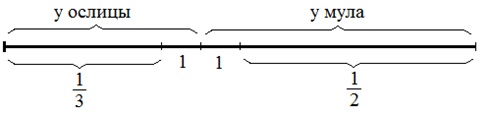
Кристина изобразила в виде отрезка общее количество мешков, показав части, принадлежащие ослице и мулу.
Если число мешков мула уменьшить на 1, то у него окажется половина всех мешков. Если число мешков ослицы уменьшить на 1, то у неё окажется треть всех мешков (у мула — в два раза больше, чем у ослицы).
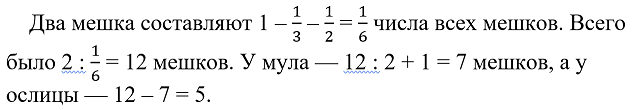
Похожие задачи встречались и у более поздних авторов. У Бхаскары (Индия, 1114 – 1185), у И. Ньютона (1642 – 1727), у Л. Эйлера (1707 – 1783).
2. (6 кл., 1273) Задача Бхаскары. Некто сказал другу: «Дай мне 100 рупий, и я стану вдвое богаче тебя». Друг ответил: «Дай ты мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?
3. (5 кл., 1145) Из «Всеобщей арифметики» И. Ньютона. Некто желает распределить между бедными деньги. Если бы у него было на восемь динаров больше, то он мог бы дать каждому по три, но он раздаёт лишь по два, и у него ещё остаётся три. Сколько бедных?
4. (6 кл., 1275) Задача Л Эйлера. Мул и осёл несли груз весом в несколько сотен каких-то единиц. Осёл, жалуясь на свою судьбу, сказал мулу: «Мне нужно только сто единиц твоей ноши, чтобы моя стала вдвое тяжелей твоей». На это мул ему ответил: «Да, это так, но если бы ты мне отдал сто единиц из твоей ноши, то я был бы нагружен втрое больше тебя». Какого веса была ноша осла и ноша мула?
Была задача такого рода и в наиболее известном российском учебник «Арифметика» Л.Ф. Магницкого (1703 г.).
5. (9 кл., 1188) Некто желает дать милостыню убогим, дав каждому по 3 пенязи (деньги), но недостаёт денег на 3 человека. Если бы дал им по 2 пенязи, тогда бы осталось денег на 4 человека. Спрашивается, сколько было убогих и сколько у того мужа было денег.
Название денария Великого княжества Литовского пе́нязь (польск. pieniądz), пришло, видимо, из задачи более раннего времени.
Представим, что сначала тот муж дал каждому человеку по 2 пенязя. Осталось на 4 человека — 2 ∙ 4 = 8 пенязей. Если к этому добавить ещё 3 ∙ 3 = 9 пенязей (для раздачи по 3 не хватало на трёх человек), то 8 + 9 = 17 пенязей хватило бы, чтобы каждому добавить ещё по 1 пенязю. То есть было 17 убогих и 17 ∙ 2 + 8 = 42 пенязя.
Соглашусь, что рассуждение получилось сложное, что данную задачу проще решить уравнением 3(x – 3) = 2(x + 4), где x — число убогих.
Но вернёмся в I–II века нашей эры, в Китай.
6. (6 кл., 1252) Китай, I в. Сообща покупают вещь. Если каждый внесёт по 8 (денежных единиц), то избыток равен 3. Если каждый внесёт по 7, то недостаток равен 4. Спрашивается количество людей и стоимость вещи.
Представим, что сначала каждый внёс по 7, и не хватило 4 денежных единиц. Со скольких человек нужно взять ещё по одной денежной единице ( 8 – 7 = 1), чтобы покрыть недостаток 4 единицы, да ещё осталось 3 единицы.
1) 3 + 4 = 7 (человек),
2) 7 ∙ 7 + 4 = 53 (денежных единиц).
7. (6 кл., 1253) Китай, II в. Сообща покупают курицу. Если каждый человек внесёт по 9 (денежных единиц), то останется 11. Если же каждый человек внесёт по 6, то не хватит 16. Найти число людей и стоимость курицы.
8. (9 кл., 1190) Китай, II в. Сообща покупают буйвола. Если каждые семь семей внесут по 190 (денежных единиц), то недостаток равен 330. Если каждые девять семей внесут по 270, то избыток равен 30. Сколько семей и сколько стоит буйвол?

Если кому милее линейные уравнения и их системы, то он всё-таки должен согласиться, что иногда арифметический способ решения может пригодиться для проверки применения уравнений и их систем. А уравнения и их системы учащиеся тоже должны освоить. Это будет тем легче сделать, чем лучше они разовьют свои способности искать арифметические способы решения задач, дающие для развития творческих способностей гораздо больше, чем следование алгоритмам решения задач при помощи уравнений.
Теги: арифметические способы решения задач, математика, старинные задачи
