Медианы треугольника и задачи на площадь
Поводом для заметки послужила следующая задача, встреченная в Интернете.
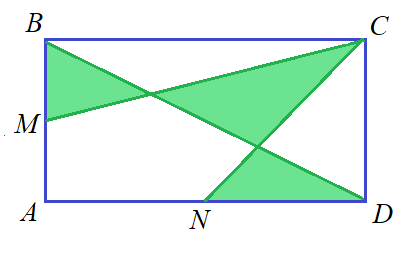
1. Какую часть площади прямоугольника ABCD составляет сумма площадей закрашенных треугольников, если M и N — середины сторон AB и AD соответственно?
Эту задачу мы решим чуть позже для общего случая — для параллелограмма. А пока повторим основные факты, которые потребуются в решении.
Свойство медиан треугольника
1) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Этот факт доказан в одном учебнике для 8 класса с помощью теоремы Фалеса, в другом с помощью подобия треугольников. Оба раза сначала доказывают, что две медианы делятся точкой их пересечения в отношении 2 : 1, считая от вершины, а потом, что третья медиана проходит через точку пересечения двух первых медиан.
Свойства площади треугольника
2) Медиана треугольника делит его площадь пополам.
3) Прямая, выходящая из вершины треугольника и делящая его сторону в отношении
m : n, делит его площадь в том же отношении.
Поупражняемся в применении приведённых свойств.
2. Докажите свойство медиан треугольника, используя свойства площади.
Пусть медианы CE и BD треугольника ABC пересекаются в точке M, а луч AM пересекает сторону BC в точке F.
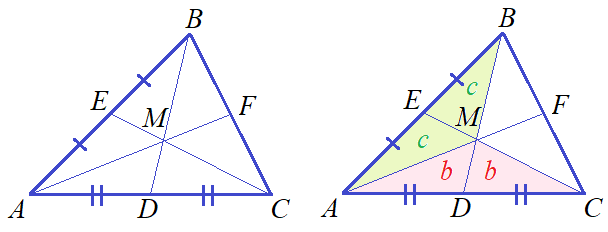
Из свойства 2) следует, что площади треугольников AEM и BEM равны — обозначим их c. Аналогично площади треугольников ADM и CDM равны — обозначим их b. Из того же свойства площади следует, что площади треугольников ABD и ACE равны — они составляют половину площади S треугольника ABC. Тогда из равенства b + 2c = 2b + c следует, что b = c = S/6.
Из утверждения, обратного свойству 3) (оно доказывается от противного), следует, что BM : MD = CM : ME = 2c : c = 2 : 1. То есть две медианы делятся точкой их пересечения в отношении 2 : 1, считая от вершины.
Медиана CE делит медиану BD в отношении 2 : 1, считая от вершины. Аналогично доказывается, что медиана, проведённая из вершины A, делит медиану BD в отношении
2 : 1, считая от вершины, то есть эта медиана проходит через точку F, а значит, совпадает с отрезком AF. Так же доказывается, что медиана CE делит медиану AF в отношении 2 : 1, считая от вершины, что и требовалось доказать.
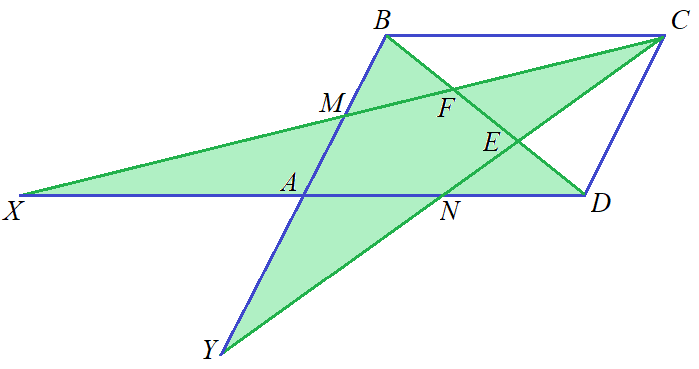
3. Какую часть площади параллелограмма ABCD составляет сумма площадей закрашенных треугольников, если M и N — середины сторон AB иAD соответственно?
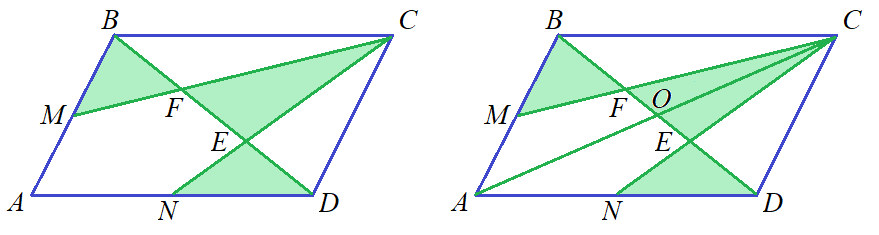
Пусть O — точка пересечения параллелограмма. Так как F — точка пересечения медиан треугольника ABC, то площади треугольников MBF и OFC равны — они составляют 1/6 площади треугольников ABC и 1/12 площади параллелограммаABCD. Аналогично площади треугольников NED и OEC равны и составляют 1/12 площади параллелограммаABCD. Тогда сумма площадей закрашенных фигур равна 4/12 = 1/3 площади параллелограммаABCD.
Ответ. 1/3.
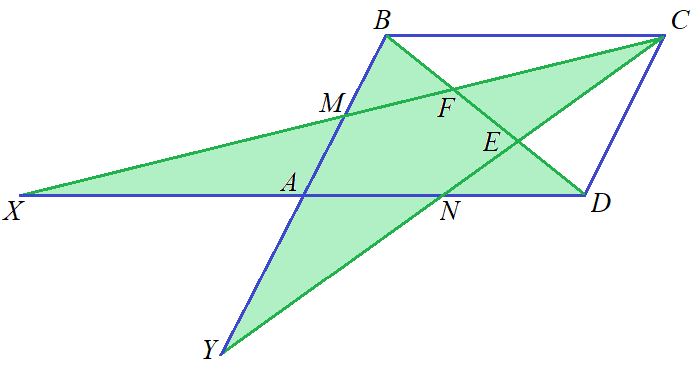
4. Какую часть площади закрашенной фигуры составляет площадь параллелограмма ABCD, если M и N — середины сторон AB иAD соответственно?