Исследовательские задачи для школьников (класс 5+)
На школьном туре Всероссийской олимпиады школьников по математике 2014-2015 года была такая задача.
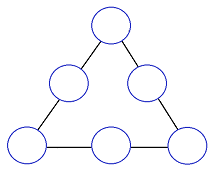
1. В шести кружках, расположенных в форме равностороннего треугольника, расставьте числа 31, 32, 33, 34, 35, 36 так, чтобы сумма чисел на всех трёх сторонах треугольника была одинаковой и равнялась 100.
Если отбросить у каждого числа по 3 десятка, то задача сведётся к расстановке чисел 1, 2, 3, 4, 5, 6 так, чтобы их сумма на каждой стороне треугольника была равна 10. Как только мы найдём способ расставить эти числа требуемым способом, так, приписав к каждому числу 3 десятка, получим решение задачи 1.
Задача станет ещё интереснее, если мы снимем ограничение по сумме.
2. В шести кружках, расположенных в форме равностороннего треугольника, расставьте числа 1, 2, 3, 4, 5, 6 так, чтобы сумма чисел на всех трёх сторонах треугольника была одинаковой. Сколько решений имеет задача? Два решения считаются одинаковыми, если они дают одинаковую «цепочку» (последовательность) чисел, при чтении по или против часовой стрелки от одного и того же числа, стоящего в вершине треугольника.
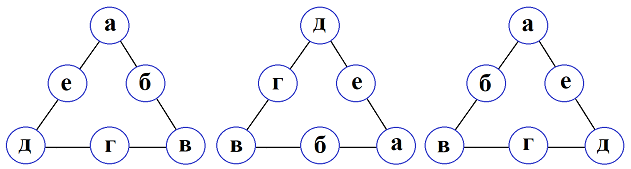
На рисунке числа заменены буквами, чтобы не портить читателю удовольствия найти решение самостоятельно. На первом и на втором рисунке буквы читаем по часовой стрелке, на третьем — против часовой стрелки, от одной и той же буквы а, стоящей в вершине треугольника. Получаем одну и ту же последовательность букв: а, б, в, г, д, е. На трёх рисунках приведено одно и то же решение.
Если дети постарше и знают про поворот и про симметрию относительно прямой, объяснение совпадения решений может быть иным: одно решение не должно получаться из другого поворотом или симметрией треугольника относительно прямой (или при последовательном выполнении этих преобразований).
Дополнение от 31.07.2020. Добавляю ещё четыре задачи.
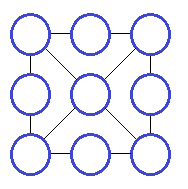
3. В девяти кружках (см. рис.) расставьте числа от 1 до 9 так, чтобы сумма трёх чисел на всех сторонах квадрата и на его диагоналях была одинаковой. Сколько решений имеет задача?
4. В восьми вершинах куба (см. рис.) расставьте числа от 1 до 8 так, чтобы сумма четырёх чисел на каждой из шести граней куба была одинаковой. Сколько решений имеет задача?
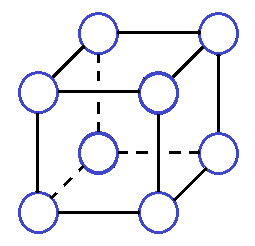
5. В восьми вершинах куба надо расставить числа от 1 до 8 так, чтобы сумма четырёх чисел при каждой вершине куба (число, стоящее в этой вершине, и три числа в соседних вершинах) была одинаковой для всех восьми вершин. Существует ли хотя бы одно решение этой задачи?
6. На шести гранях куба надо расставить числа от 1 до 6 так, чтобы сумма трёх чисел на гранях, при каждой вершине куба была одинаковой для всех восьми вершин куба. Существует ли хотя бы одно решение этой задачи?
Теги: головоломка, задача, математика, олимпиада по математике
